题目内容
平行六面体ABCD-A1B1C1D1中，以顶点A为端点的三条棱，两两夹角都为60°，且AB=AD=1，AA1=2，求对角线AC1的长．
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：由
2=（
+
+
）2，利用向量求解．
| AC1 |
| AB |
| BC |
| CC1 |
解答：
解：平行六面体ABCD-A1B1C1D1中，
∵以顶点A为端点的三条棱，两两夹角都为60°，
且AB=AD=1，AA1=2，
∴
2=（
+
+
）2
=1+1+4+2×1×1×cos60°+2×1×2×cos60°+2×1×2×cos60°
=11，
∴|
|=
．
∴线段AC1的长度为
．
∵以顶点A为端点的三条棱，两两夹角都为60°，
且AB=AD=1，AA1=2，
∴
| AC1 |
| AB |
| BC |
| CC1 |
=1+1+4+2×1×1×cos60°+2×1×2×cos60°+2×1×2×cos60°
=11，
∴|
| AC1 |
| 11 |
∴线段AC1的长度为
| 11 |
点评：本题考查线段长的求法，是基础题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
快捷英语周周练系列答案
相关题目
若a＞b，则下列各项正确的是（ ）
| A、ac＞bc |
| B、ax2＞bx2 |
| C、a2＞b2 |
| D、a2x＞b2x |
正方体ABCD-A1B1C1D1的面BCC1B1内有一点M，满足∠MD1D=∠BD1D，则点M的轨迹是（ ）
| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
将点P（-2，2）变换为P′（-6，1）的伸缩变换公式为（ ）
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
将6个相同的小球放入3个不同的盒子，要求每个盒子中至少有1个小球，且每个盒子中的小球个数都不同，则不同的放法共有（ ）
| A、4种 | B、6种 | C、8种 | D、10种 |
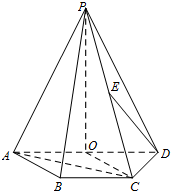如图，四棱锥P-ABCD中，底面ABCD是直角梯形，CD⊥平面PAD，BC∥AD，PA=PD，O，E分别为AD，PC的中点，PO=AD=2BC=2CD．
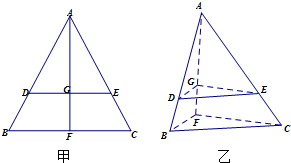在等边三角形ABC中，D、E分别是AB、BC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF折起，得到如图乙所示的三棱锥A-BCF．
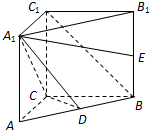（理科）如图，在直三棱柱ABC-A1B1C1中，∠ACB=
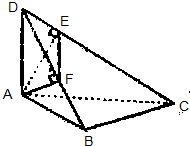如图，在四边形ABCD中，DA⊥平面ABC，∠ABC=90°，AE⊥CD，AF⊥DB，求证：