已知y∈R.复数z=i.当y为何值时:(1)z∈R?(2)z是纯虚数? 题目和参考答案——青夏教育精英家教网—

题目内容

10．已知y∈R，复数z=（2+2y）+（y-1）i，当y为何值时：
（1）z∈R？
（2）z是纯虚数？

分析（1）直接由虚部为0求得y值；
（2）由实部为0且虚部不为0列式求解．

解答解：（1）若z=（2+2y）+（y-1）i为实数，则y-1=0，得y=1；
（2）由$\left\{\begin{array}{l}{2+2y=0}\\{y-1≠0}\end{array}\right.$，解得y=-1．

点评本题考查复数的基本概念，是基础的计算题．

练习册系列答案

1．已知圆C₁：（x+1）²+（y-1）²=4，圆C₂与圆C₁关于直线x-y-1=0对称，则圆C₂的方程为（　　）

18．椭圆$\left\{\begin{array}{l}x=5cosφ\\ y=3sinφ\end{array}\right.（φ为参数）$的焦点坐标为（　　）

5．已知扇形AOB的周长是6，中心角是2弧度，则该扇形的面积为$\frac{9}{4}$．

15．

某市有6条南北向街道，4条东西向街道，图中共有m个矩形，从A点走到B点最短路线的走法有n种，则m，n的值分别为（　　）

2．已知函数φ（x）=$\frac{a}{x+1}$，a为常数．
（1）若f（x）=lnx+φ（x），且a=$\frac{9}{2}$，求函数f（x）的单调区间；
（2）若g（x）=|lnx|+φ（x），且对任意x₁，x₂∈[1，2]，x₁≠x₂，都有$\frac{g（{x}_{2}）-g（{x}_{1}）}{{x}_{2}-{x}_{1}}$＜-1，求a的取值范围．

19．

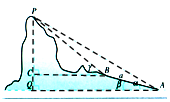如图，在山脚A测得山顶P的仰角为60°，沿倾斜角为15°的斜坡向上走200米到B，在B处测得山顶P的仰角为75°，则山高h=150（$\sqrt{6}$+$\sqrt{2}$）米．

20．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为120°，且|$\overrightarrow{a}$|=2，|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2$\sqrt{7}$，则|$\overrightarrow{b}$|=4．

试题分类