题目内容
11.数列{an}中,a1=1,a2=2,数列{bn}满足bn=an+1+(-1)nan,n∈N*.(Ⅰ)若数列{an}是等比数列,an=32,求项数n的值;
(Ⅱ)若数列{bn}是常数列,求数列{an}的前2016项的和S2016.
分析 (I)利用等比数列的通项公式即可得出.
(II)由数列{bn}是常数列,可得b1=a2-a1=1.利用an+1+(-1)nan=1,n∈N*.可得a2k+1+a2k=1,a2k-a2k-1=1,k∈N*.a2k+1=-a2k-1,a2k+a2k+2=2.分组求和即可得出.
解答 解:(I)数列{an}是等比数列,
∴an=32=${a}_{1}(\frac{{a}_{2}}{{a}_{1}})^{n-1}$=2n-1,
解得n=6.
(II)∵数列{bn}是常数列,
b1=a2-a1=1,
∴an+1+(-1)nan=1,n∈N*.
∴a2k+1+a2k=1,a2k-a2k-1=1,k∈N*.
∴a2k+1=-a2k-1,a2k+a2k+2=2.
∴数列{an}的前2016项的和S2016=(a1+a3)+(a5+a7)+…+(a2013+a2015)+(a2+a4)+…+(a2014+a2016)
=0+2×504=1008.
点评 本题考查了等比数列的通项公式、分类讨论方法、分组求和方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.直线3x-4y-4=0被圆x2+y2-6x=0截得的弦长为( )
| A. | $2\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 2 |
2.已知实数a、b满足a2+b2=1,设函数f(x)=x2-4x+5,则使f(a)≥f(b)的概率为( )
| A. | $\frac{3}{4}+\frac{1}{2π}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}+\frac{1}{π}$ |
19.(文科)学业水平考试后,某校对高二学生的数学、英语成绩进行了统计,结果如下(人数):
已知英语、数学的优秀率分别为24%、30%(注:合格人数中不包含优秀人数).
(1)求a、b的值;
(11)现按照英语成绩的等级,采用分层抽样的方法,从数学不合格的学生中选取6人,若再从这6人中任选2人,求这两名学生的英语成绩恰为一人优秀一人合格的概率.
| 项目 | 数学 | |||
| 优秀 | 合格 | 不合格 | ||
| 英 语 | 优秀 | 70 | 30 | 20 |
| 合格 | 60 | 240 | b | |
| 不合格 | a | 20 | 10 | |
(1)求a、b的值;
(11)现按照英语成绩的等级,采用分层抽样的方法,从数学不合格的学生中选取6人,若再从这6人中任选2人,求这两名学生的英语成绩恰为一人优秀一人合格的概率.
20.执行如图所示的程序框图.若输出的结果为3,则可输入的实数x的个数为( )
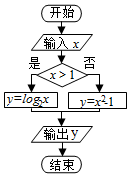

| A. | l | B. | 2 | C. | 3 | D. | 4 |
1.圆(x+1)2+(y+2)2=4与圆(x-2)2+(y-2)2=9的公切线有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
