题目内容
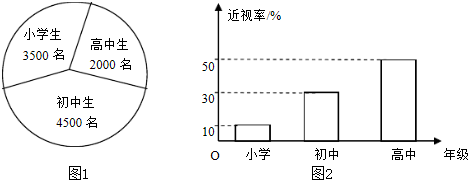
已知某地区中小学学生的近视情况分布如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )

| A、200,20 |
| B、100,20 |
| C、200,10 |
| D、100,10 |
考点:频率分布直方图
专题:概率与统计
分析:根据图1可得总体个数,根据抽取比例可得样本容量,计算分层抽样的抽取比例,求得样本中的高中学生数,再利用图2求得样本中抽取的高中学生近视人数.
解答:
解:由图1知:总体个数为3500+2000+4500=10000,
∴样本容量=10000×2%=200,
分层抽样抽取的比例为
,
∴高中生抽取的学生数为40,
∴抽取的高中生近视人数为40×50%=20.
故选:A.
∴样本容量=10000×2%=200,
分层抽样抽取的比例为
| 1 |
| 50 |
∴高中生抽取的学生数为40,
∴抽取的高中生近视人数为40×50%=20.
故选:A.
点评:本题借助图表考查了分层抽样方法,熟练掌握分层抽样的特征是关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
为了得到函数y=sin3x+cos3x的图象,可以将函数y=
cos3x的图象( )
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知命题:p:对任意x∈R,总有|x|≥0,q:x=1是方程x+2=0的根;则下列命题为真命题的是( )
| A、p∧¬q | B、¬p∧q |
| C、¬p∧¬q | D、p∧q |
4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设z=
+i,则|z|=( )
| 1 |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |