题目内容
已知三棱锥A-BCD内接于球O,AB=AD=AC=BD=
,∠BCD=60°,则球O的表面积为 .
| 3 |
考点:球内接多面体,球的体积和表面积
专题:计算题,空间位置关系与距离
分析:画出图形,求出底面三角形的外接圆的半径,求出A到底面BCD的距离,然后得外接球的半径,即可求解表面积.
解答:
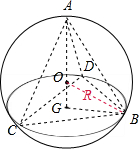 解:如图:底面△BCD中,BD=
解:如图:底面△BCD中,BD=
,∠BCD=60°,
∴GB=r=
=1,
∵AB=AD=AC=BD=
,A-BCD是圆锥,
∴AG⊥平面BCD,并且经过球的球心O,
则AG=
=
,
设球的半径为R,
OB2=OG2+GB2,即R2=(
-R)2+1,
解得R=
,
∴球O的表面积为:4πR2=4π×(
)2=
π.
故答案为:
π.
 解:如图:底面△BCD中,BD=
解:如图:底面△BCD中,BD=| 3 |
∴GB=r=
| ||
| 2sin60° |
∵AB=AD=AC=BD=
| 3 |
∴AG⊥平面BCD,并且经过球的球心O,
则AG=
| AB2-GB2 |
| 2 |
设球的半径为R,
OB2=OG2+GB2,即R2=(
| 2 |
解得R=
3
| ||
| 4 |
∴球O的表面积为:4πR2=4π×(
3
| ||
| 4 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题考查球O的表面积的求法,几何体的外接球与几何体的关系,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
已知某地区中小学学生的近视情况分布如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
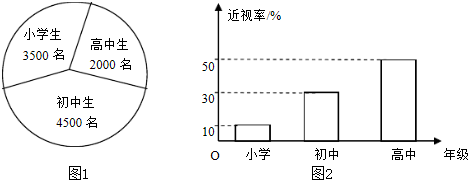

| A、200,20 |
| B、100,20 |
| C、200,10 |
| D、100,10 |
执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )


A、s>
| ||
B、s>
| ||
C、s>
| ||
D、s>
|
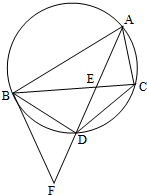 如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论: