题目内容

若函数f（x）=2sin（
π
6
x+
π
3
）（2＜x＜10）的图象与x轴交于点A，过点A的直线l与f（x）的图象交于B、C两点，O为坐标原点，则（
OB
+
OC
）•
OA
=
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据“f（x）=2sin（
π
6
x+
π
3
）（2＜x＜10）的图象与x轴交于点A”求出A点坐标，设B（x1，y1），C（x2，y2），由正弦函数的对称性可知B，C 两点关于A对称即x1+x2=8，y1+y2=0，代入向量的数量积的坐标表示即可求解
解答： 解：由f（x）=2sin（
π
6
x+
π
3
）=0，可得
π
6
x+
π
3
=kπ，
∴x=6k-2，k∈Z
∵2＜x＜10
∴x=4即A（4，0）
设B（x1，y1），C（x2，y2）
∵过点A的直线l与函数的图象交于B、C两点
∴B，C 两点关于A对称即x1+x2=8，y1+y2=0
∴（
OB
+
OC
）•
OA
=（x1+x2，y1+y2）•（4，0）=4（x1+x2）=32
故答案为：32．
点评：本题主要考查了向量的数量积的坐标表示，解题的关键正弦函数对称性质的应用．
练习册系列答案
相关题目
设F1，F2分别是椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，过点F1的直线交椭圆E于A，B两点，|AF1|=3|F1B|．
（Ⅰ）若|AB|=4，△ABF2的周长为16，求|AF2|；
（Ⅱ）若cos∠AF2B=
3
5
，求椭圆E的离心率．
在平面直角坐标系中，O为原点，A（-1，0），B（0，
3
），C（3，0），动点D满足|
CD
|=1，则|
OA
+
OB
+
OD
|的最大值是
 
．
在平面直角坐标系xOy中，直线x+2y-3=0被圆（x-2）2+（y+1）2=4截得的弦长为
 
．
若△ABC的内角满足sinA+
2
sinB=2sinC，则cosC的最小值是
 
．
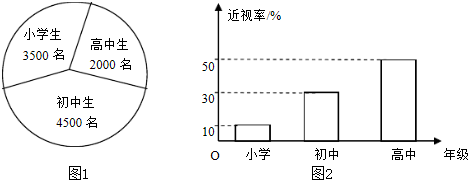
已知某地区中小学学生的近视情况分布如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为（　　）
A、200，20
B、100，20
C、200，10
D、100，10
已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=
1
2
（|x-a2|+|x-2a2|-3a2），若?x∈R，f（x-1）≤f（x），则实数a的取值范围为（　　）
A、[-
1
6
，
1
6
]
B、[-
6
6
，
6
6
]
C、[-
1
3
，
1
3
]
D、[-
3
3
，
3
3
]
平面向量
a
=（1，2），
b
=（4，2），
c
=m
a
+
b
（m∈R），且
c
与
a
的夹角等于
c
与
b
的夹角，则m=（　　）
A、-2B、-1C、1D、2
设m、n是两条不同的直线，α，β是两个不同的平面，则（　　）
A、若m⊥n，n∥α，则m⊥α
B、若m∥β，β⊥α，则m⊥α
C、若m⊥β，n⊥β，n⊥α，则m⊥α
D、若m⊥n，n⊥β，β⊥α，则m⊥α

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网