题目内容
已知命题:p:对任意x∈R,总有|x|≥0,q:x=1是方程x+2=0的根;则下列命题为真命题的是( )
| A、p∧¬q | B、¬p∧q |
| C、¬p∧¬q | D、p∧q |
考点:复合命题的真假
专题:简易逻辑
分析:判定命题p,q的真假,利用复合命题的真假关系即可得到结论.
解答:
解:根据绝对值的性质可知,对任意x∈R,总有|x|≥0成立,即p为真命题,
当x=1时,x+2=3≠0,即x=1不是方程x+2=0的根,即q为假命题,
则p∧¬q,为真命题,
故选:A.
当x=1时,x+2=3≠0,即x=1不是方程x+2=0的根,即q为假命题,
则p∧¬q,为真命题,
故选:A.
点评:本题主要考查复合命题的真假关系的应用,先判定p,q的真假是解决本题的关键,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知某地区中小学学生的近视情况分布如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
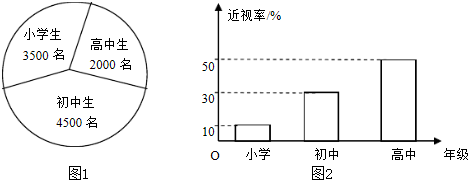

| A、200,20 |
| B、100,20 |
| C、200,10 |
| D、100,10 |
已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=
(|x-a2|+|x-2a2|-3a2),若?x∈R,f(x-1)≤f(x),则实数a的取值范围为( )
| 1 |
| 2 |
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )


A、s>
| ||
B、s>
| ||
C、s>
| ||
D、s>
|
平面向量
=(1,2),
=(4,2),
=m
+
(m∈R),且
与
的夹角等于
与
的夹角,则m=( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| A、-2 | B、-1 | C、1 | D、2 |
根据如下样本数据,得到回归方程
=bx+a,则( )
 |
| y |
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A、a>0,b>0 |
| B、a>0,b<0 |
| C、a<0,b>0 |
| D、a<0,b<0 |
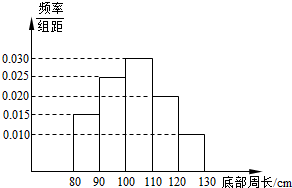 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有