题目内容
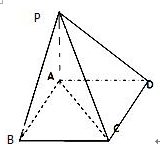
AB为⊙O的一定直径，CD为⊙O上一动直径，过点D作线段AB的垂线DE，延长ED到点P，使|PD|=|AB|，求证：直线CP必定过一定点．
考点：与圆有关的比例线段
专题：空间位置关系与距离
分析：连接CP中点M与圆心O，OM为△CPD的中位线，从而OM=r（半径），进而M在圆O上，由此能证明直线CP必定过一定点．
解答：
证明：连接CP中点M与圆心O，
∵CD为直径，∴O为直径CD中点，
∴OM为△CPD的中位线，
∴OM=
DP=
CD=r（半径），
∴M在圆O上，
∵DE⊥AB，
∴OM⊥AB，
∵AB为定直径，
∴M点始终为定点，
∴直线CP必定过一定点M．
∵CD为直径，∴O为直径CD中点，
∴OM为△CPD的中位线，
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
∴M在圆O上，
∵DE⊥AB，
∴OM⊥AB，
∵AB为定直径，
∴M点始终为定点，
∴直线CP必定过一定点M．
点评：本题考查直线必过一定点的证明，是中档题，解题时要注意圆的性质的合理运用．
练习册系列答案
相关题目
函数y=x+
（x＞0）的最小值是（ ）
| 1 |
| x |
| A、1 | B、2 | C、-2 | D、以上都不对 |
若sinx+siny=1，则cosx+cosy的取值范围是（ ）
| A、[-2，2] | ||||
| B、[-1，1] | ||||
C、[0，
| ||||
D、[-
|
设集合A={1，2，3}，B={x|x（x-2）＜0}，则A∩B=（ ）
| A、{1，2，3} |
| B、{2，3} |
| C、{1} |
| D、{1，2} |
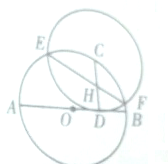如图所示，在圆O上任取C点为圆心，作一圆C与圆O的直径AB相切于D，圆C与圆O交于E，F，且EF与CD相交于H．求证：EF平分CD．