题目内容
若sinαcosα=-
，α∈（
，π），则sinα-cosα= ．
| 1 |
| 8 |
| π |
| 2 |
考点：三角函数的化简求值
专题：计算题,三角函数的求值
分析：由已知先确定sinα-cosα的符号，根据同角三角函数的关系即可求值．
解答：
解：∵α∈（
，π），
∴sinα＞0，cosα＜0，sinα-cosα＞0
∵sinαcosα=-
，
∴sinα-cosα=
=
=
故答案为：
| π |
| 2 |
∴sinα＞0，cosα＜0，sinα-cosα＞0
∵sinαcosα=-
| 1 |
| 8 |
∴sinα-cosα=
| (sinα-cosα)2 |
| 1-2sinαcosα |
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题主要考察了同角三角函数的关系式的应用，属于基本知识的考查．
练习册系列答案
相关题目
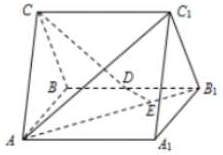如图，直三棱柱ABC-A1B1C1中，AC=BC，C到AB的距离大于1，AA1=AB=2，D为BB1的中点，E为AB1上的一点，AE=3EB1．