题目内容
如图所示,直线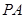 垂直于⊙
垂直于⊙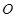 所在的平面,
所在的平面,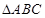 内接于⊙
内接于⊙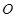 ,且
,且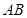 为⊙
为⊙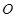 的直径,点
的直径,点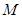 为线段
为线段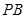 的中点.现有结论:①
的中点.现有结论:①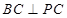 ;②
;② 平面
平面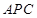 ;③点
;③点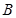 到平面
到平面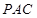 的距离等于线段
的距离等于线段 的长.其中正确的是( )
的长.其中正确的是( )
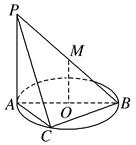
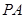 垂直于⊙
垂直于⊙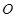 所在的平面,
所在的平面,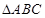 内接于⊙
内接于⊙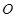 ,且
,且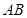 为⊙
为⊙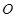 的直径,点
的直径,点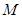 为线段
为线段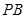 的中点.现有结论:①
的中点.现有结论:①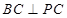 ;②
;② 平面
平面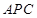 ;③点
;③点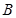 到平面
到平面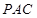 的距离等于线段
的距离等于线段 的长.其中正确的是( )
的长.其中正确的是( )
| A.①② | B.①②③ | C.① | D.②③ |
B
试题分析:对于结论①,由于
 是以
是以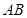 为直径的圆
为直径的圆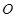 上一点,所以
上一点,所以 ,因为
,因为 平面
平面 ,于是可以得到
,于是可以得到 ,结合直线与平面垂直的判定定理可以得到
,结合直线与平面垂直的判定定理可以得到 平面
平面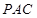 ,因此
,因此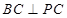 ,所以结论①正确;对于结论②,由于
,所以结论①正确;对于结论②,由于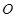 、
、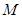 分别为
分别为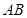 、
、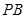 的中点,由中位线原理可知
的中点,由中位线原理可知 ,利用直线与平面平行的判定定理可以得到
,利用直线与平面平行的判定定理可以得到 平面
平面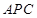 ,所以结论②正确;对于结论③,由结论①知,
,所以结论②正确;对于结论③,由结论①知, 平面
平面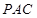 ,所以结论③正确,故选B.
,所以结论③正确,故选B.
练习册系列答案
相关题目

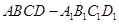 中
中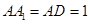 ,
,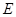 为
为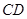 中点.
中点.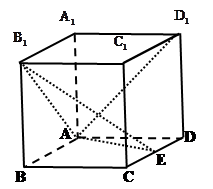
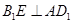 ;
;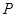 ,使得
,使得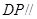 平面
平面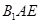 ?若存在,求
?若存在,求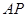 的长;若不存在,说明理由;
的长;若不存在,说明理由;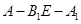 的大小为
的大小为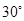 ,求
,求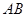 的长.
的长.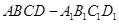 中,已知平面
中,已知平面 ,且
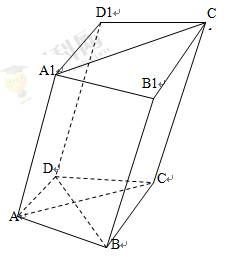
,且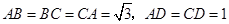 .
.
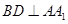 ;
;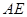 ∥平面
∥平面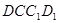 ,求
,求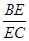 的值.
的值.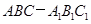 中,
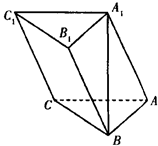
中,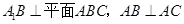 .
.
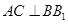 ;
;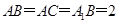 ,在棱
,在棱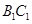 上确定一点P, 使二面角
上确定一点P, 使二面角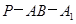 的平面角的余弦值为
的平面角的余弦值为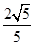 .
.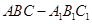 的侧面
的侧面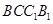 是菱形,
是菱形,

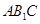
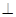 平面
平面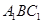 ;
;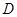 是
是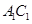 上的点,且
上的点,且 平面
平面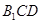 ,求
,求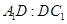 的值.
的值.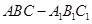 中,
中,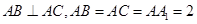 ,点
,点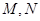 分别为
分别为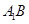 和
和 的中点.
的中点.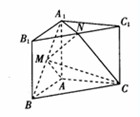
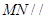 平面
平面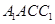 ;
;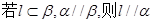 ②
②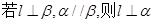
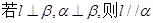 ④
④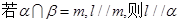
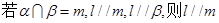
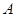 、
、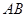 为正方体的两个顶点,
为正方体的两个顶点,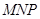 、
、 、
、 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出