题目内容
19.已知O为坐标原点,F是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM与y轴交点为N,且$\overrightarrow{EO}=3\overrightarrow{NO}$,则C的离心率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 根据椭圆的几何性质,由PF⊥x轴设M(-c,t),
写出直线AM的方程,求出AM与y轴的交点E的坐标;
再写出直线BM的方程,求出BM与y轴的交点N的坐标;
根据$\overrightarrow{EO}=3\overrightarrow{NO}$列出方程求出$\frac{c}{a}$的值.
解答 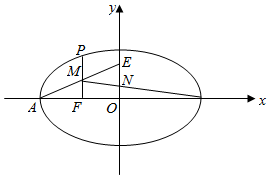 解:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),
解:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),
且A(-a,0),B(a,0);
由PF⊥x轴,不妨设M(-c,t),(t≠0);
则直线AM的方程为$\frac{y}{t}$=$\frac{x+a}{-c+a}$,
令x=0,得y=$\frac{at}{a-c}$,
∴直线AM与y轴的交点为E(0,$\frac{at}{a-c}$);
又直线BM的方程为$\frac{y}{t}$=$\frac{x-a}{-c-a}$,
令x=0,得y=$\frac{at}{a+c}$,
∴直线BM与y轴的交点为N(0,$\frac{at}{a+c}$);
又$\overrightarrow{EO}=3\overrightarrow{NO}$,
∴$\frac{at}{a-c}$=$\frac{3at}{a+c}$,
化简得a=2c,
∴$\frac{c}{a}$=$\frac{1}{2}$,
则曲线C的离心率为$\frac{1}{2}$.
故选:B.
点评 本题主要考查了椭圆离心率的计算问题,根据条件求出直线方程和点N,E的坐标是解题的关键.

练习册系列答案
相关题目
20.f(x)是定义在R上的奇函数,当x>0时,(x2+l)f′(x)+2xf(x)<0,且f(2)=0.则不等式f(x)<0的解集是( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
14.在一次共有15000名考生的某市高二的联考中,这些学生的数学成绩ξ服从正态分布 N(100,δ2),且p(80<ξ≤100)=0.35.若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上的试卷中抽取( )
| A. | 20份 | B. | 15份 | C. | 10份 | D. | 5份 |
11.已知直线l过点P(1,1),且与曲线y=x3在点P处的切线互相垂直,则直线l的方程为( )
| A. | x+3y+4=0 | B. | x+3y-4=0 | C. | 3x-y+2=0 | D. | 3x-y-2=0 |
8.已知复数z满足z•i=1+2i,则在复平面内,z所对应的点的坐标是( )
| A. | (2,1) | B. | (1,2) | C. | (-1,2) | D. | (2,-1) |
9.已知Sn是等差数列{an}的前n项和,且a1=1,S6=3S3,则S9=( )
| A. | 9 | B. | 15 | C. | 21 | D. | 27 |