题目内容
已知直线x+y+m=0与圆x2+y2=4交于不同的两点A,B,O是坐标原点,
+
|≥|
|,则实数m的取值范围是( )
| |OA |
| OB |
| AB |
| A、[-2,2] | ||||
B、[2,2
| ||||
C、(-2
| ||||
D、[2,2
|
考点:两向量的和或差的模的最值
专题:平面向量及应用
分析:设AB线段的中点为C,可得2|
|≥|
|,可得
≤OC<2,利用圆心到直线的距离公式列出关于m的不等关系,求解即可得到实数m的取值范围.
| OC |
| AB |
| 2 |
解答:
解:∵直线x+y+m=0与圆x2+y2=4交于不同的两点A,B,
故AB为圆的一条弦,且圆心O(0,0),半径r=2,
设线段AB的中点为C,根据向量加法的平行四边形法则,可得
+
=2
,
∴
+
|≥|
|,即为2|
|≥|
|,即|
|≥
|
|=AC,
根据圆中弦的性质,则△OAC为直角三角形,
∴在Rt△OAC中,OA=r=2,OC≥AC,
∴
≤OC<2,
∵OC为点O到直线x+y+m=0的距离,
故OC=
=
,
∴
≤
<2,即
,解得m∈(-2
,-2]∪[2,2
),
∴实数m的取值范围是(-2
,-2]∪[2,2
).
故选:B.
故AB为圆的一条弦,且圆心O(0,0),半径r=2,
设线段AB的中点为C,根据向量加法的平行四边形法则,可得
| OA |
| OB |
| OC |
∴
| |OA |
| OB |
| AB |
| OC |
| AB |
| OC |
| 1 |
| 2 |
| AB |
根据圆中弦的性质,则△OAC为直角三角形,
∴在Rt△OAC中,OA=r=2,OC≥AC,
∴
| 2 |
∵OC为点O到直线x+y+m=0的距离,
故OC=
| |0+0+m| | ||
|
| |m| | ||
|
∴
| 2 |
| |m| | ||
|
|
| 2 |
| 2 |
∴实数m的取值范围是(-2
| 2 |
| 2 |
故选:B.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,绝对值不等式的解法,向量的和与向量的模.本题解题的关键是将|
+
|≥|
|,转化为
≤|
|<2.属于中档题.
| OA |
| OB |
| AB |
| 2 |
| OC |

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
已知三角形ABC中,
•
<0,则三角形ABC的形状为( )
| BA |
| BC |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰直角三角形 |
一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是( )
A、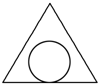 |
B、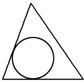 |
C、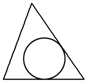 |
D、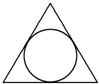 |
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于( )cm3.


| A、18 | B、21 | C、24 | D、28 |
用“辗转相除法”求得3459和3357的最大公约数是( )
| A、3 | B、9 | C、17 | D、51 |