题目内容
12.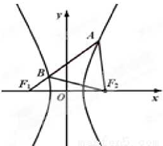 如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 8 | B. | 8$\sqrt{2}$ | C. | 8$\sqrt{3}$ | D. | 16 |
分析 由双曲线的定义,可得F1A-F2A=F1A-AB=F1B=2a,BF2-BF1=2a,BF2=4a,F1F2=2c,再在△F1BF2中应用余弦定理得,a,c的关系,即可求出△BF1F2的面积.
解答 解:因为△ABF2为等边三角形,不妨设AB=BF2=AF2=m,
A为双曲线上一点,F1A-F2A=F1A-AB=F1B=2a,
B为双曲线上一点,则BF2-BF1=2a,BF2=4a,F1F2=2c,
在△F1BF2中应用余弦定理得:4c2=4a2+16a2-2•2a•4a•cos120°,
得c2=7a2,
在双曲线中:c2=a2+b2,b2=24
∴a2=4
∴△BF1F2的面积为$\frac{1}{2}•2a•4a•\frac{\sqrt{3}}{2}$=$2\sqrt{3}{a}^{2}$=2$\sqrt{3}$×4=8$\sqrt{3}$.
故选:C.
点评 本题给出经过双曲线左焦点的直线被双曲线截得弦AB与右焦点构成等边三角形,求三角形的面积,着重考查了双曲线的定义和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
2.若函数y=$\sqrt{3}{sin^2}x+sinx•cosx-\frac{{\sqrt{3}}}{2}$的图象关于直线x=φ对称,则x=φ可以为( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |