题目内容
2.若函数y=$\sqrt{3}{sin^2}x+sinx•cosx-\frac{{\sqrt{3}}}{2}$的图象关于直线x=φ对称,则x=φ可以为( )| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
分析 由三角函数恒等变换的应用化简函数解析式,利用正弦函数的对称性,代入x的值函数取得最值,然后即可求得φ的值.
解答 解:∵y=$\sqrt{3}{sin^2}x+sinx•cosx-\frac{{\sqrt{3}}}{2}$=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=sin(2x-$\frac{π}{3}$),
又∵图象关于直线x=φ对称,
∴f(φ)=sin(2×φ-$\frac{π}{3}$)=±1,可得:2×φ-$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,
解得:φ=$\frac{kπ}{2}$+$\frac{5π}{12}$,k∈Z,可得当k=0时,x=φ=$\frac{5π}{12}$.
故选:A.
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的对称性,考查了转化思想,属于基础题.

练习册系列答案
相关题目
7.“%”运算使(1,3)%[2,4]=(1,2),(2,5)%(4,5)=(2,4],则{1,2,3,4,5}%{1,3,5}%{2,4,6}=( )
| A. | {1,2,3,4,5,6} | B. | ∅ | C. | {2,4} | D. | {1,3,5} |
11.已知y=f(x)是定义在[-1,1]上的偶函数,与g(x)图象关于x=1对称,当x∈[2,3]时,g(x)=2a(x-2)-3(x-2)2,a为常数,若f(x)的最大值为12,则a=( )
| A. | 3 | B. | 6 | C. | 6或$\frac{15}{2}$ | D. | $\frac{15}{2}$ |
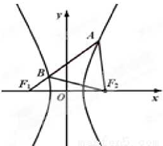 如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )