题目内容
4.定义在R上的函数f(x)的导函数为f'(x),且满足f(3)=1,f(-2)=3,当x≠0时有x•f'(x)>0恒成立,若非负实数a、b满足f(2a+b)≤1,f(-a-2b)≤3,则$\frac{b+2}{a+1}$的取值范围为$[{\frac{4}{5},3}]$.分析 根据x•f'(x)>0恒成立得到函数的单调性,从而将f(2a+b)≤1化成f(2a+b)≤f(3),得到0≤2a+b≤3,同理化简f(-a-2b)≤3,得到-2≤-a-2b≤0.然后在aob坐标系内作出相应的平面区域,得到如图所示的阴影部分平面区域,利用直线的斜率公式即可求出$\frac{b+2}{a+1}$的取值范围.
解答 解:由x•f'(x)>0恒成立可得: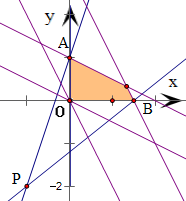
当x∈(-∞,0)时,f′(x)<0,f(x)单调递减,
当x∈(0,+∞)时,f′(x)>0,f(x)单调递增,
又∵a,b为非负实数,
∴f(2a+b)≤1可化为f(2a+b)≤1=f(3),可得0≤2a+b≤3,
同理可得-2≤-a-2b≤0,即0≤a+2b≤2,
作出以及a≥0和b≥0所对应的平面区域,
得到如图的阴影部分区域,
解之得A(0,1)和B(1.5,0)
而等于可行域内的点与P(-1,-2)连线的斜率,
结合图形可知:kPB是最小值,kPA是最大值,
由斜率公式可得:kPA=$\frac{1+2}{0+1}$=3,kPB=$\frac{0+2}{1.5+1}$=$\frac{4}{5}$,
故$\frac{b+2}{a+1}$的取值范围为[$\frac{4}{5}$,3]
故答案为:$[{\frac{4}{5},3}]$
点评 本题在给出函数的导数图象基础之上,求满足不等式组的$\frac{b+2}{a+1}$的取值范围.着重考查了利用导数研究函数的单调性、直线的斜率公式和二元一元不等式组表示的平面区域等知识,属于中档题.

练习册系列答案
相关题目
12.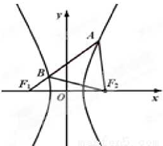 如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )
 如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左右两支分别交于点B,A两点.若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 8 | B. | 8$\sqrt{2}$ | C. | 8$\sqrt{3}$ | D. | 16 |
19.设集合M={x|x2-2ax-1≤0,a>0},集合N={x|x2+2x-3>0},若M∩N中恰有一个整数,则实数a的取值范围是( )
| A. | (1,+∞) | B. | $(0,\frac{3}{4})$ | C. | $[\frac{3}{4},\frac{4}{3})$ | D. | $[\frac{3}{4},+∞)$ |
9.一元二次方程x2+(2k-1)x+k2=0两个根均大于1的充分必要条件是( )
| A. | k<-2 | B. | k<-3 | C. | k<0 | D. | k>2 |
14.S=(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1)+1,则合并同类项后S=( )
| A. | (x-2)5 | B. | (x+1)5 | ||
| C. | x5 | D. | x5+5x4+10x3+10x2+5x+1 |