题目内容
17．已知a，b，c均为直线，α，β为平面，下面关于直线与平面关系的命题：①任意给定一条直线与一个平面α，则平面α内必存在与a垂直的直线；
②a∥β，β内必存在与a相交的直线；
③α∥β，a?α，b?β，必存在与a，b都垂直的直线；
其中正确命题的个数为（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
分析 由空间中直线与平面的位置关系逐个分析命题得答案．
解答 解：①任意给定一条直线与一个平面α，则平面α内必存在与a垂直的直线，正确；
②a∥β，则a与β无公共点，β内不存在与a相交的直线，故②错误；
③α∥β，a?α，b?β，与两个平面垂直的直线，与直线a，b垂直，故必存在与a，b都垂直的直线，故③正确．
∴正确命题的个数有2个．
故选：C．
点评 本题考查了空间中直线与平面的位置关系，考查了空间想象能力和思维能力，是中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
7．“%”运算使（1，3）%[2，4]=（1，2），（2，5）%（4，5）=（2，4]，则{1，2，3，4，5}%{1，3，5}%{2，4，6}=（ ）
| A． | {1，2，3，4，5，6} | B． | ∅ | C． | {2，4} | D． | {1，3，5} |
12．
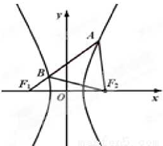如图，F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1（a＞0，b＞0）的左、右焦点，过F1的直线l与双曲线的左右两支分别交于点B，A两点．若△ABF2为等边三角形，则△BF1F2的面积为（ ）
如图，F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{24}}$=1（a＞0，b＞0）的左、右焦点，过F1的直线l与双曲线的左右两支分别交于点B，A两点．若△ABF2为等边三角形，则△BF1F2的面积为（ ）| A． | 8 | B． | 8$\sqrt{2}$ | C． | 8$\sqrt{3}$ | D． | 16 |
9．一元二次方程x2+（2k-1）x+k2=0两个根均大于1的充分必要条件是（ ）
| A． | k＜-2 | B． | k＜-3 | C． | k＜0 | D． | k＞2 |
6．已知集合U={x|x＞0}，∁UA={x|0＜x＜3}，那么集合A=（ ）
| A． | {x|x＞3} | B． | {x|x≥3} | C． | {x|x＜0或x＞3} | D． | {x|x≤0或x≥3} |