题目内容
1.数列{an}中,${a_1}=\frac{1}{2},{a_{n+1}}=\frac{{n{a_n}}}{{({n+1})({n{a_n}+1})}}({n∈{N^*}})$,若不等式$\frac{3}{n^2}+\frac{1}{n}+t{a_n}≥0$恒成立,则实数t的取值范围是[-$\frac{15}{2}$,+∞)..分析 由题意可知,两边取倒数可得:则$\frac{1}{(n+1){a}_{n+1}}$-$\frac{1}{n{a}_{n}}$=1,又$\frac{1}{1•{a}_{1}}$=2,
数列{$\frac{1}{n{a}_{n}}$}是以2为首项,1为公差的等差数列,利用等差数列的通项公式即可得出an.不等式$\frac{3}{n^2}+\frac{1}{n}+t{a_n}≥0$化为:t≥-(n+$\frac{3}{n}$+4).再利用基本不等式的性质即可得出实数t的取值范围.
解答 解:∵an+1=$\frac{n{a}_{n}}{(n+1)(n{a}_{n}+1)}$(n∈N*),
∴$\frac{1}{{a}_{n+1}}$=$\frac{(n+1)n{a}_{n}+(n+1)}{n{a}_{n}}$=(n+1)+$\frac{n+1}{n{a}_{n}}$,
即$\frac{1}{(n+1){a}_{n+1}}$-$\frac{1}{n{a}_{n}}$=1,又$\frac{1}{1•{a}_{1}}$=2,
∴数列{$\frac{1}{n{a}_{n}}$}是以2为首项,1为公差的等差数列,
∴$\frac{1}{n{a}_{n}}$=2+(n-1)=n+1,
∴an=$\frac{1}{n(n+1)}$.
∵不等式$\frac{3}{n^2}+\frac{1}{n}+t{a_n}≥0$化为:t≥-(n+$\frac{3}{n}$+4).
∵n+$\frac{3}{n}$+4≥2$\sqrt{n×\frac{3}{n}}$+4=4+2$\sqrt{3}$,当且仅当n=$\frac{3}{n}$时取等号,
由n∈N*,则当n=2时,n+$\frac{3}{n}$+4取最小,最小值为$\frac{15}{2}$
∴t≥-$\frac{15}{2}$,
故答案为:[-$\frac{15}{2}$,+∞).
点评 本题考查了等差数列的通项公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
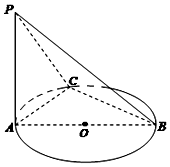 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | $({\sqrt{5},2\sqrt{5}})$ | B. | $({2\sqrt{5},5})$ | C. | $({\sqrt{5},5})$ | D. | $({2,\sqrt{5}})$ |