题目内容
17.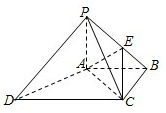 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.(1)求证:PD∥平面EAC.
(2)求平面ACE和平面ABCD所成锐二面角的余弦值.
分析 (1)根据线面平行的判定定理即可证明PD∥平面EAC.
(2)建立坐标系,求出平面的法向量,利用向量法即可求平面ACE和平面ABCD所成锐二面角的余弦值.
解答 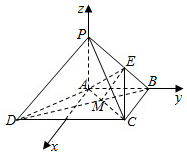 证明:(1)∵AB⊥BC,AB=BC=1,∴AC=$\sqrt{2}$,∠BAC=$\frac{π}{4}$,
证明:(1)∵AB⊥BC,AB=BC=1,∴AC=$\sqrt{2}$,∠BAC=$\frac{π}{4}$,
∵AC=AD,AC⊥AD,
∴CD=2,∠ACD=$\frac{π}{4}$
∴∠BAC=∠ACD,则AB∥CD,
连接BD,交AC于M,连EM,则$\frac{DM}{MB}=\frac{CD}{AB}=2$,
又PE=2EB,在△BPD中,$\frac{PE}{EB}=\frac{DM}{MB}=2$,
∴PD∥EM,
∵PD?平面EAC,EM?平面EAC,
∴PD∥平面EAC
(2)建立如图所示的空间坐标系如图:
则A(0,0,0),P(0,0,1),B(0,1,0),C(1,1,0),E(0,$\frac{2}{3}$,$\frac{1}{3}$),
设$\overrightarrow{m}$=(x,y,z)是平面AEC的一个法向量,
则$\overrightarrow{AE}$=(1,1,0),$\overrightarrow{AE}$(0,$\frac{2}{3}$,$\frac{1}{3}$),
则$\overrightarrow{m}$•$\overrightarrow{AE}$=x+y=0,$\overrightarrow{m}$•$\overrightarrow{AE}$=$\frac{2}{3}$y+$\frac{1}{3}$z=0,
得$\left\{\begin{array}{l}{x=-y}\\{z=-2y}\end{array}\right.$,
令y=1,则x=-1,z=-2,则$\overrightarrow{m}$=(-1,1,-2),
同理平面ABCD的法向量为$\overrightarrow{n}$=$\overrightarrow{AP}$=(0,0,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\sqrt{6}}{3}$,
即平面ACE和平面ABCD所成锐二面角的余弦值是$\frac{\sqrt{6}}{3}$.
点评 本题主要考查空间直线和平面位置关系的判断以及二面角的求解,建立坐标系,求出平面的法向量,利用向量法是解二面角的常用方法.综合性较强,运算量较大.

 阅读快车系列答案
阅读快车系列答案| A. | 若f1(-1)=f1(1),则f(-1)>f(1) | B. | 若f2(-1)=f2(1),则f(-1)>f(1) | ||
| C. | 若f(-1)=f(1),则f2(-1)>f2(1) | D. | 若f2(1)=f1(-1),则f1(-1)<f1(1) |
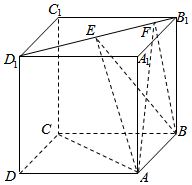 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )| A. | AC⊥BF | B. | 三棱锥A-BEF的体积为定值 | ||
| C. | EF∥平面ABCD | D. | 面直线AE、BF所成的角为定值 |
| A. | (2,4] | B. | [-1,2] | C. | [-1,4] | D. | (4,+∞) |
 如图,在多面体ABCDE中,BD⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
如图,在多面体ABCDE中,BD⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.