题目内容
2.已知二次函数f(x)=ax2+bx(|b|≤2|a|),定义f1(x)=max{f(t)|-1≤t≤x≤1},f2(x)=min{f(t)|-1≤t≤x≤1},其中max{a,b}表示a,b中的较大者,min{a,b}表示a,b中的较小者,则下列命题正确的是( )| A. | 若f1(-1)=f1(1),则f(-1)>f(1) | B. | 若f2(-1)=f2(1),则f(-1)>f(1) | ||
| C. | 若f(-1)=f(1),则f2(-1)>f2(1) | D. | 若f2(1)=f1(-1),则f1(-1)<f1(1) |
分析 由新定义可知f1(-1)=f2(-1)=f(-1),f(x)在[-1,1]上的最大值为f1(1),最小值为f2(1).
解答 解:(1)若f1(-1)=f1(1),则f(-1)为f(x)在[-1,1]上的最大值,
∴f(-1)>f(1)或f(-1)=f(1).故A错误;
(2)若f2(-1)=f2(1),则f(-1)是f(x)在[-1,1]上的最小值,
∴f(-1)<f(1)或f(-1)=f(1),故B错误.
(3)若f(-1)=f(1),则f(x)关于y轴对称,
∴当a>0时,f2(1)=f(0)≠f(-1)=f2(-1),故C错误.
(4)若f2(1)=f1(-1),则f(-1)为f(x)在[-1,1]上的最小值,
而f1(-1)=f(-1),f1(1)表示f(x)在[-1,1]上的最大值,
∴f1(-1)<f1(1).故D正确.
故选:D.
点评 本题考查了对于新定义的理解和二次函数的图象与性质,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
10.设集合A={x|y=$\sqrt{2x{-x}^{2}}$.x∈N},B={x|y=ln(2-x)},则A∩B表示的集合为( )
| A. | {1} | B. | {x|0≤x<2} | C. | {0,1} | D. | {0,1,2} |
13.已知集合A={1,2,3,4},集合B={x|x∈A,且2x∉A},则A∩B=( )
| A. | {1,2} | B. | {1,3} | C. | {2,4} | D. | {3,4} |
7.设m为不小于2的正整数,对任意n∈Z,若n=qm+r(其中q,r∈Z,且0≤r<m),则记fm(n)=r,如f2(3)=1,f3(8)=2,下列关于该映射fm:Z→Z的命题中,不正确的是( )
| A. | 若a,b∈Z,则fm(a+b)=fm(a)+fm(b) | |
| B. | 若a,b,k∈Z,且fm(a)=fm(b),则fm(ka)=fm(kb) | |
| C. | 若a,b,c,d∈Z,且fm(a)=fm(b),fm(c)=fm(d),则fm(a+c)=fm(b+d) | |
| D. | 若a,b,c,d∈Z,且fm(a)=fm(b),fm(c)=fm(d),则fm(ac)=fm(bd) |
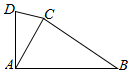 在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=150°,∠BAC=60°,AC=2,AB=$\sqrt{3}$+1.
在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=150°,∠BAC=60°,AC=2,AB=$\sqrt{3}$+1.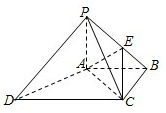 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.