题目内容
12.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow a$|=1,$|2\overrightarrow a-\overrightarrow b|$=$2\sqrt{3}$,$\overrightarrow a$在$\overrightarrow b$方向的投影为$\frac{1}{2}$,则$\overrightarrow b•(\overrightarrow a+2\overrightarrow b)$=34.分析 根据投影的定义和向量模的计算,求出|$\overrightarrow{b}$|=4,$\overrightarrow{a}•\overrightarrow{b}$=2,即可求出答案.
解答 解:∵|$\overrightarrow a$|=1,$|2\overrightarrow a-\overrightarrow b|$=$2\sqrt{3}$,$\overrightarrow a$在$\overrightarrow b$方向的投影为$\frac{1}{2}$,
∴$|2\overrightarrow a-\overrightarrow b|$2=4|$\overrightarrow a$|2-4$\overrightarrow{a}•\overrightarrow{b}$+|$\overrightarrow{b}$|2=12,$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{1}{2}$,
∴|$\overrightarrow{b}$|=4,$\overrightarrow{a}•\overrightarrow{b}$=2,
∴$\overrightarrow b•(\overrightarrow a+2\overrightarrow b)$=$\overrightarrow{a}•\overrightarrow{b}$+2|$\overrightarrow{b}$|2=2+2×16=34,
故答案为:34.
点评 本题考查向量垂直的充要条件、考查向量模的平方等于向量的平方、考查向量的数量积公式.

练习册系列答案
相关题目
1.已知数列{an}是等差数列,且a7-2a4=6,a3=2,则公差d=( )
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 8 | D. | 16 |
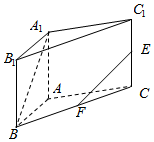 直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求:
直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求: 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.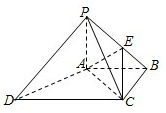 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.