题目内容
8. 如图,在多面体ABCDE中,BD⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
如图,在多面体ABCDE中,BD⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.(1)若是F线段DC的中点,证明:EF⊥面DBC;
(2)求多面体ABCDE的体积.
分析 (1)根据线面直线的判定定理以及直线平行的性质即可证明EF⊥面DBC;
(2)利用转化法结合四棱锥的体积公式即可求多面体ABCDE的体积.
解答 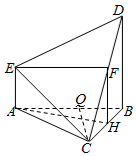 证明:(1)∵△ABC是边长为2的等边三角形,
证明:(1)∵△ABC是边长为2的等边三角形,
∴取BC的中点H,连接FH,AH,
若是F线段DC的中点,
则FH是△BCD的中位线,
∴FH∥BD,FH=$\frac{1}{2}$BD=1,
∵AE∥DB,∴AE∥FH,
∵2AE=2,∴AE=1,
则AE=FH=1,
则四边形AEFH是平行四边形,
则EF∥AH,
∵BD⊥平面ABC,∴FH⊥平面ABC,
∴平面ABC⊥平面BCD,
∵在正三角形ABC中,AH⊥BC,
∴AH⊥面DBC,
∵EF∥AH,
∴EF⊥面DBC;
(2)取AB的中点O,连接CO,则CO⊥AB,
∵BD⊥平面ABC,BD?平面ABDE,
∴平面ABC⊥平面ABDE,
则CO⊥平面ABDE,
则CO是C到平面ABDE的距离,则CO=$\sqrt{3}$,
则梯形ABDE的面积S=$\frac{AE+BE}{2}×AB$=$\frac{1+2}{2}×2=3$,
则多面体ABCDE的体积V=$\frac{1}{3}{S}_{ABDE}•CO$=$\frac{1}{3}×3×\sqrt{3}=\sqrt{3}$.
点评 本题主要考查线面垂直的判定以及多面体的体积的计算,根据线面垂直的判定定理以及转化法是解决本题的关键.考查学生的运算能力.

练习册系列答案
相关题目
13.已知集合A={1,2,3,4},集合B={x|x∈A,且2x∉A},则A∩B=( )
| A. | {1,2} | B. | {1,3} | C. | {2,4} | D. | {3,4} |
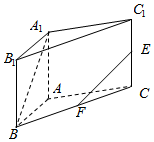 直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求:
直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=2$\sqrt{2}$,E,F分别是CC1,BC的中点,求: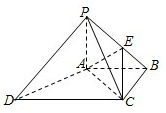 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.