题目内容
5.求曲线y=sinx,直线x=0,x=$\frac{π}{2}$以及x轴所围成平面图形的面积1.分析 根据积分的应用可知所求的面积为,然后根据积分公式进行计算即可.
解答 解:∵在[0,$\frac{π}{2}$],sinx≥0,
∴y=sinx在[0,$\frac{π}{2}$]上与x轴所围成的平面图形的面积S=${∫}_{0}^{\frac{π}{2}}$sinxdx=(-cosx)|${\;}_{0}^{\frac{π}{2}}$=-cos$\frac{π}{2}$+cos0=1.
故答案为:1.
点评 本题考查了定积分的几何意义及其求法,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.设集合A={x|y=$\sqrt{2x{-x}^{2}}$.x∈N},B={x|y=ln(2-x)},则A∩B表示的集合为( )
| A. | {1} | B. | {x|0≤x<2} | C. | {0,1} | D. | {0,1,2} |
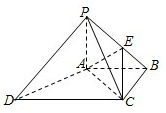 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AD,AB⊥BC,PA=AB=BC=1,AC=AD,点E在棱PB上,且PE=2EB.