题目内容
选修4-5；不等式选讲
已知a＞0，b＞0，a+b=1，求证：
（Ⅰ）
+
+
≥8；
（Ⅱ）（1+
）（1+
）≥9．
已知a＞0，b＞0，a+b=1，求证：
（Ⅰ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
（Ⅱ）（1+
| 1 |
| a |
| 1 |
| b |
考点：不等式的证明
专题：证明题,综合法
分析：（Ⅰ）利用基本不等式，先证明
≥4，即可得出结论；
（Ⅱ）（1+
）（1+
）=
+
+
+1，由（Ⅰ）可知
+
+
≥8，即可得出结论．
| 1 |
| ab |
（Ⅱ）（1+
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
解答：
证明：（Ⅰ）∵a+b=1，
∴ab≤(
)2=
，
∴
≥4，∴
+
+
=
+
=
≥8；
（Ⅱ）（1+
）（1+
）=
+
+
+1
由（Ⅰ）可知
+
+
≥8
∴
+
+
+1≥9，
∴（1+
）（1+
）≥9．
∴ab≤(
| a+b |
| 2 |
| 1 |
| 4 |
∴
| 1 |
| ab |
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
| a+b |
| ab |
| 1 |
| ab |
| 2 |
| ab |
（Ⅱ）（1+
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
由（Ⅰ）可知
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| ab |
∴（1+
| 1 |
| a |
| 1 |
| b |
点评：本题考查不等式的证明，考查综合法的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
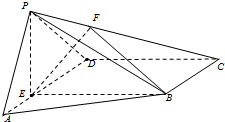如图，在四棱锥P-ABCD中，E为AD上一点，PE⊥平面ABCD，AD∥BC，AD⊥CD，BC=ED=2AE，F为PC上一点，且CF=2FP．
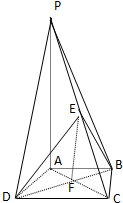如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=2，AD=4，DC=3，PA=5，E∈PC，AC∩BD=F．
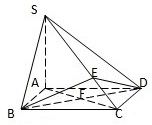已知四棱锥S-ABCD的底面ABCD是正方形，SA⊥底面ABCD，E是SC上的任意一点．
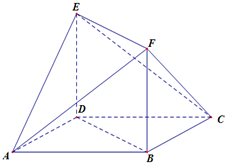如图所示的多面体中，ABCD是菱形，BDEF是矩形，ED⊥平面ABCD，