题目内容
已知函数f(x)=|x-2|+2|x-a|(a∈R).
(Ⅰ)当a=1时,解不等式f(x)>3;
(Ⅱ)不等式f(x)≥1在区间(-∞,+∞)上恒成立,求实数a的取值范围.
(Ⅰ)当a=1时,解不等式f(x)>3;
(Ⅱ)不等式f(x)≥1在区间(-∞,+∞)上恒成立,求实数a的取值范围.
考点:函数恒成立问题
专题:计算题,分类讨论,不等式的解法及应用
分析:(Ⅰ)按照x≤1,1<x≤2,x>2三种情况进行讨论,去掉绝对值符号可解不等式,注意三种情况要对x的范围取并集;
(Ⅱ)f(x)≥1即|x-2|+2|x-a|≥1,易知|x-2|≥1即x≤1或x≥3时,|x-2|+2|x-a|≥1对任意实数a恒成立,从而丨x-2丨+2丨x-a丨≥1 对任意实数x恒成立,只须丨x-2丨+2丨x-a丨≥1 对x∈(1,3)恒成立.按照x∈(1,2],x∈(2,3)两种情况讨论去掉绝对值符号,分离出参数a后转化为函数的最值可得a的范围,最后取交集可得;
(Ⅱ)f(x)≥1即|x-2|+2|x-a|≥1,易知|x-2|≥1即x≤1或x≥3时,|x-2|+2|x-a|≥1对任意实数a恒成立,从而丨x-2丨+2丨x-a丨≥1 对任意实数x恒成立,只须丨x-2丨+2丨x-a丨≥1 对x∈(1,3)恒成立.按照x∈(1,2],x∈(2,3)两种情况讨论去掉绝对值符号,分离出参数a后转化为函数的最值可得a的范围,最后取交集可得;
解答:
解:(Ⅰ)当a=1时,f(x)=|x-2|+2|x-1|,
①当x≤1时,f(x)=2-x+2(1-x)=-3x+4,
由f(x)>3,得-3x+4>3,解得x<
,
∴x<
;
②1<x≤2时,f(x)=2-x+2(x-1)=x,
由f(x)>3,得x>3,
∴此时不等式无解;
③当x>2时,f(x)=x-2+2(x-1)=3x-4,
由f(x)>3,得3x-4>3,解得x>
,
∴x>
;
综上,不等式f(x)>3的解集为(-∞,
)∪(
,+∞).
(Ⅱ)f(x)≥1即|x-2|+2|x-a|≥1,
当|x-2|≥1,即x≤1或x≥3时,显然|x-2|+2|x-a|≥1对任意实数a恒成立;
∴丨x-2丨+2丨x-a丨≥1 对任意实数x恒成立,只须丨x-2丨+2丨x-a丨≥1 对x∈(1,3)恒成立.
(1)若x∈(1,2]时,得2|x-a|≥x-1,即a≥
,或a≤
,x∈(1,2]恒成立,则a≥
,或a≤1;
(2)若当x∈(2,3)时,得2|x-a|≥3-x,即a≥
,或a≤
对x∈(2,3)恒成立,则a≥3,或a≤
;
对(1)(2)中a的范围取交集,得a≤1或a≥3.
①当x≤1时,f(x)=2-x+2(1-x)=-3x+4,
由f(x)>3,得-3x+4>3,解得x<
| 1 |
| 3 |
∴x<
| 1 |
| 3 |
②1<x≤2时,f(x)=2-x+2(x-1)=x,
由f(x)>3,得x>3,
∴此时不等式无解;
③当x>2时,f(x)=x-2+2(x-1)=3x-4,
由f(x)>3,得3x-4>3,解得x>
| 7 |
| 3 |
∴x>
| 7 |
| 3 |
综上,不等式f(x)>3的解集为(-∞,
| 1 |
| 3 |
| 7 |
| 3 |
(Ⅱ)f(x)≥1即|x-2|+2|x-a|≥1,
当|x-2|≥1,即x≤1或x≥3时,显然|x-2|+2|x-a|≥1对任意实数a恒成立;
∴丨x-2丨+2丨x-a丨≥1 对任意实数x恒成立,只须丨x-2丨+2丨x-a丨≥1 对x∈(1,3)恒成立.
(1)若x∈(1,2]时,得2|x-a|≥x-1,即a≥
| 3x-1 |
| 2 |
| x+1 |
| 2 |
| 5 |
| 2 |
(2)若当x∈(2,3)时,得2|x-a|≥3-x,即a≥
| x+3 |
| 2 |
| 3x-3 |
| 2 |
| 3 |
| 2 |
对(1)(2)中a的范围取交集,得a≤1或a≥3.
点评:对于含有绝对值的题目,本身就是分类的,问题的提出已包含了分类的原因.分类讨论是一种逻辑方法,是一种重要的数学思想,同时也是一种重要的解题策略,它体现了化整为零、积零为整的思想与归类整理的方法,在高考试题中占有重要的位置.

练习册系列答案
相关题目
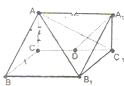 已知三棱柱ABC-A1B1C1的底面为直角三角形,则棱与底面垂直,如图所示,D是棱CC1的中点,且∠ACB=90°,BC=1,AC=
已知三棱柱ABC-A1B1C1的底面为直角三角形,则棱与底面垂直,如图所示,D是棱CC1的中点,且∠ACB=90°,BC=1,AC= 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,E为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,E为PD的中点.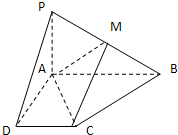 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=