题目内容
13.如图,在正方体ABCD-A′B′C′D′中,求向量$\overrightarrow{AC}$分别与向量$\overrightarrow{A′B′}$,$\overrightarrow{B′A′}$,$\overrightarrow{AD′}$,$\overrightarrow{CD′}$,$\overrightarrow{B′D′}$的夹角.
分析 由$\overrightarrow{{A}^{'}{B}^{'}}$=$\overrightarrow{AB}$,得∠BAC是向量$\overrightarrow{AC}$分别与向量$\overrightarrow{A′B′}$的夹角,由$\overrightarrow{{B}^{'}{A}^{'}}$=-$\overrightarrow{AB}$,得∠BAC是向量$\overrightarrow{AC}$分别与向量$\overrightarrow{A′B′}$的夹角的补角,由已知∠CAD′是向量$\overrightarrow{AC}$与向量$\overrightarrow{AD′}$的夹角,∠ACD′是向量$\overrightarrow{AC}$与向量$\overrightarrow{CD′}$的夹角,由$\overrightarrow{BD}=\overrightarrow{{B}^{'}{D}^{'}}$,AC⊥BD,得$\overrightarrow{AC}$与向量$\overrightarrow{B′D′}$的夹角,由此能求出结果.
解答 解:∵$\overrightarrow{{A}^{'}{B}^{'}}$=$\overrightarrow{AB}$,∴∠BAC是向量$\overrightarrow{AC}$分别与向量$\overrightarrow{A′B′}$的夹角,
∵AB=BC,AB⊥BC,
∴∠BAC=45°,
∴向量$\overrightarrow{AC}$与向量$\overrightarrow{A′B′}$的夹角为45°;
∵$\overrightarrow{{B}^{'}{A}^{'}}$=-$\overrightarrow{AB}$,∴∠BAC是向量$\overrightarrow{AC}$分别与向量$\overrightarrow{A′B′}$的夹角的补角,
∵AB=BC,AB⊥BC,
∴∠BAC=45°,
∴向量$\overrightarrow{AC}$与向量$\overrightarrow{B′A′}$的夹角为135°;
∠CAD′是向量$\overrightarrow{AC}$与向量$\overrightarrow{AD′}$的夹角,∠ACD′是向量$\overrightarrow{AC}$与向量$\overrightarrow{CD′}$的夹角,
∵AD′=AC=D′C,∴∠CAD′=∠ACD'=60°,
∴向量$\overrightarrow{AC}$与向量$\overrightarrow{AD′}$的夹角为60°,向量$\overrightarrow{AC}$与向量$\overrightarrow{CD′}$的夹角为120°;
∵$\overrightarrow{BD}=\overrightarrow{{B}^{'}{D}^{'}}$,AC⊥BD,∴$\overrightarrow{AC}$与向量$\overrightarrow{B′D′}$的夹角为90°.
点评 本题考查向量与向量的夹角的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | 没有零点 | B. | 有且仅有一个零点 | ||
| C. | 有且仅有两个零点 | D. | 有无穷多个零点 |
| A. | 21008 | B. | 21008i | C. | -21008 | D. | -21008i |
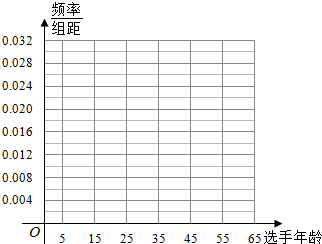 《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:| 选手年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 6 | 22 | 32 | 24 | 10 | 6 |
(Ⅱ)已知样本中年龄在[55,65]内的6位选手中,有4名女选手,2名男选手,现从中选3人进行回访,记选出的女选手的人数为X,求X的分布列、数学期望与方差.