题目内容
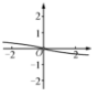
5.若函数f(x)=x|x-a|(a>0)在区间[1,2]上的最小值为2,则a=3.分析 由a>0,结合y=f(x)的图象可得f(x)在[1,2]的最小值可以是f(1),或f(2),f(a).分别计算求得a,将绝对值去掉,运用二次函数的对称轴和区间的关系,结合单调性,即可判断a的值.
解答 解:由a>0,结合y=f(x)的图象可得f(x)在[1,2]的最小值
可以是f(1),或f(2),f(a).
由f(a)=0,不成立;
由f(1)=|1-a|=2,解得a=-1(舍去)或a=3,
当a=3时,f(x)=x|x-3|在[1,2],即有:f(x)=x(3-x)在[1,2]递减,
可得f(1)或f(2)取得最小值,且为2;
由f(2)=2|2-a|=2,解得a=1或a=3.
当a=3时,f(x)=x|x-3|在[1,2]即为:f(x)=x(3-x)在[1,2]递减,
可得f(1)或f(2)取得最小值,且为2;
当a=1时,f(x)=x|x-1|在[1,2]即为:f(x)=x(x-1),
可得f(x)在[1,2]递增,即有f(1)取得最小值,且为0,不成立.
综上可得a=3.
故答案为:3.
点评 本题考查函数的最值的求法,注意运用分类讨论的思想方法,考查二次函数的最值的求法,注意讨论对称轴和区间的关系,属于中档题.

练习册系列答案
相关题目
15.若复数z满足iz=2-4i,则$\overline{z}$在复平面内对应的点的坐标是( )
| A. | (2,4) | B. | (2,-4) | C. | (-4,-2) | D. | (-4,2) |
16.某高校进行自主招生测试,对20名已经选拔入围的学生进行语言能力和逻辑思维能力的测试,其测试结果对应人数如下表:
例如表中语言表达能力良好且逻辑思维能力一般的学生是4人,由于部分数据丢失,只知道从这20名参加测试的学生中随机选取1名,选到语言表达能力一般的学生的概率为$\frac{1}{4}$.
(Ⅰ)求m,n的值;
(Ⅱ)从语言表达能力为优秀的学生中随机选取2名,求其中至少有1名逻辑思维能力优秀的学生的概率.
| 逻辑思维能力 语言表达能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | m |
| 良好 | 4 | 4 | 1 |
| 优秀 | 1 | m | 2 |
(Ⅰ)求m,n的值;
(Ⅱ)从语言表达能力为优秀的学生中随机选取2名,求其中至少有1名逻辑思维能力优秀的学生的概率.
15.已知集合S={1,2,a},T={2,3,4,b},若S∩T={1,2,3},则a-b=( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |