题目内容
7.将函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得到函数f(x)的图象,则f(x)=( )| A. | cos2x | B. | sin(2x+$\frac{π}{4}$) | C. | -cos2x | D. | -sin2x |
分析 直接利用函数的图象平移原则求解.
解答 解:将函数y=sin2x的图象向左平移$\frac{π}{4}$个单位,
得f(x)=sin2(x+$\frac{π}{4}$)=sin(2x+$\frac{π}{2}$)=cos2x.
故选:A.
点评 本题考查三角函数的平移,三角函数的平移原则为左加右减上加下减,是基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17.某中学调查了某班全部50名同学参加数学兴趣小组和语文兴趣小组的情况,数据如表:(单位:人)
(1)从该班同学中随机选1名,求该同学至少参加上述一个兴趣小组的概率;
(2)在既参加数学兴趣小组,又参加语文兴趣小组的6个同学中,有4个男同学,2个女同学,现从这6个同学中随机抽取2人做进一步的调查,求抽取的2人中恰有1个女同学的概率.
| 参加数学兴趣小组 | 未参加数学兴趣小组 | |
| 参加语文兴趣小组 | 6 | 10 |
| 未参加语文兴趣小组 | 14 | 20 |
(2)在既参加数学兴趣小组,又参加语文兴趣小组的6个同学中,有4个男同学,2个女同学,现从这6个同学中随机抽取2人做进一步的调查,求抽取的2人中恰有1个女同学的概率.
18.已知a∈R,则a=1是复数$z=\frac{1+ai}{1-ai}$(i为虚数单位)为纯虚数的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
15.若复数z满足iz=2-4i,则$\overline{z}$在复平面内对应的点的坐标是( )
| A. | (2,4) | B. | (2,-4) | C. | (-4,-2) | D. | (-4,2) |
2.2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
乙电商:
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
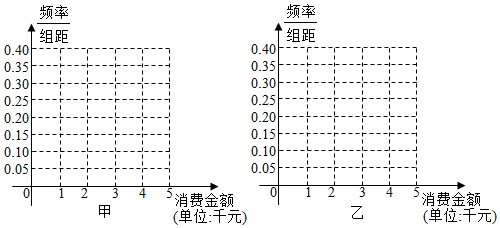
(Ⅱ)运用分层抽样分别从甲、乙1000名消费者中各自抽出20人放在一起,在抽出的40人中,从消费金额不小于4千元的人中任取2人,求这2人恰好是来自不同电商消费者的概率.
甲电商:
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |

(Ⅱ)运用分层抽样分别从甲、乙1000名消费者中各自抽出20人放在一起,在抽出的40人中,从消费金额不小于4千元的人中任取2人,求这2人恰好是来自不同电商消费者的概率.
19.已知数列{an}的前n项和Sn=an2+bn+c,则数列{an}是等差数列的充要条件为( )
| A. | a≠0,c=0 | B. | a=0,c=0 | C. | c=0 | D. | c≠0 |
16.某高校进行自主招生测试,对20名已经选拔入围的学生进行语言能力和逻辑思维能力的测试,其测试结果对应人数如下表:
例如表中语言表达能力良好且逻辑思维能力一般的学生是4人,由于部分数据丢失,只知道从这20名参加测试的学生中随机选取1名,选到语言表达能力一般的学生的概率为$\frac{1}{4}$.
(Ⅰ)求m,n的值;
(Ⅱ)从语言表达能力为优秀的学生中随机选取2名,求其中至少有1名逻辑思维能力优秀的学生的概率.
| 逻辑思维能力 语言表达能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | m |
| 良好 | 4 | 4 | 1 |
| 优秀 | 1 | m | 2 |
(Ⅰ)求m,n的值;
(Ⅱ)从语言表达能力为优秀的学生中随机选取2名,求其中至少有1名逻辑思维能力优秀的学生的概率.