题目内容
已知正数x、y满足
+
=1,则x+2y的最小值是 .
| 2 |
| x |
| 1 |
| y |
考点:函数的最值及其几何意义
专题:不等式的解法及应用
分析:利用“乘1法”和基本不等式的性质即可得出.
解答:
解:∵正数x,y满足
+
=1,
∴x+2y=(x+2y)(
+
)=4+
+
≥4+2
=4+4=8,当且仅当x=2y=4时取等号.
∴x+2y的最小值是8.
故答案为:8.
| 2 |
| x |
| 1 |
| y |
∴x+2y=(x+2y)(
| 2 |
| x |
| 1 |
| y |
| 4y |
| x |
| x |
| y |
|
∴x+2y的最小值是8.
故答案为:8.
点评:本题考查了“乘1法”和基本不等式的性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=(ex-e-x)sinx的图象(部分)大致是( )
A、 |
B、 |
C、 |
D、 |
直线y=
x与双曲线C:
+
=1(a>0,b>0)左右两支分别交于M、N两点,F为双曲线C的右焦点,O是坐标原点,若|FO|=|MO|,则双曲线的离心率等于( )
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
下列选项叙述错误的是( )
| A、命题“若x≠0,则ex≠1”的逆否命题是“若ex=1,则x=0” | ||
B、“x>2”是“
| ||
| C、若命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,使得x02+x0+1≤0 | ||
| D、若p∧q为假命题,则p,q均为假命题 |
甲、乙两人从4门课程中各选修2门,则甲、乙两人所选的课程中有一门相同的选法有( )
| A、6种 | B、12种 |
| C、16种 | D、24 |
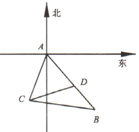 如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是
如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是