题目内容
直线y=
x与双曲线C:
+
=1(a>0,b>0)左右两支分别交于M、N两点,F为双曲线C的右焦点,O是坐标原点,若|FO|=|MO|,则双曲线的离心率等于( )
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:根据直线的斜率公式,得∠NOF=60°,所以△ONF是以c为边长的等边三角形,得点N(
c,
c),代入双曲线方程并化简整理,得关于离心率e的方程,解之可得该双曲线的离心率.
| 1 |
| 2 |
| ||
| 2 |
解答:
解: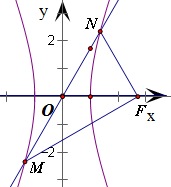 ∵直线y=
∵直线y=
x交双曲左右两支于M,N,且|OM|=|OF|,
∴由tan∠NOF=
,得∠NOF=60°,且|ON|=|OF|,
因此△ONF是以c为边长的等边三角形,
得N(
c,
c),代入双曲线方程得
-
=1
将e=
和b2=c2-a2代入化简整理,
得
e2-
•
=1,解之得e2=4±2
,
∴双曲线的离心率e=
+1(因为双曲线离心率e>1,舍去
-1)
故选B.
 ∵直线y=
∵直线y=| 3 |
∴由tan∠NOF=
| 3 |
因此△ONF是以c为边长的等边三角形,
得N(
| 1 |
| 2 |
| ||
| 2 |
| ||
| a2 |
| ||
| b2 |
将e=
| c |
| a |
得
| 1 |
| 4 |
| 3 |
| 4 |
| e2 |
| e2-1 |
| 3 |
∴双曲线的离心率e=
| 3 |
| 3 |
故选B.
点评:本题给出直线交双曲线于M、N两点,且在|ON|=c的情况下求双曲线的离心率,着重考查了双曲线的简单性质和直线与双曲线位置关系等知识,属于基础题.

练习册系列答案
相关题目
已知双曲线
-
=1的右焦点到其渐近线的距离等于
,则该双曲线的离心率等于( )
| x2 |
| 4 |
| y2 |
| m2 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
已知函数f(x)=sin(2x+φ),其中φ∈(0,2π),若f(x)≤|f(
)|对x∈R恒成立,且f(
)<f(π),则f(x)的单调递增区间是( )
| π |
| 6 |
| π |
| 2 |
A、[kπ+
| ||||
B、[kπ-
| ||||
C、[kπ,kπ+
| ||||
D、[kπ-
|
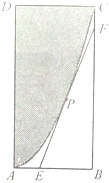 如图,有一个长方形地块ABCD,边AB为2km,AD为4km.,地块的一角是湿地(图中阴影部分),其边缘线AC是以直线AD为对称轴,以A为顶点的抛物线的一部分.现要铺设一条过边缘线AC上一点P的直线型隔离带EF,E,F分别在边AB,BC上(隔离带不能穿越湿地,且占地面积忽略不计).设点P到边AD的距离为t(单位:km),△BEF的面积为S(单位:km2).
如图,有一个长方形地块ABCD,边AB为2km,AD为4km.,地块的一角是湿地(图中阴影部分),其边缘线AC是以直线AD为对称轴,以A为顶点的抛物线的一部分.现要铺设一条过边缘线AC上一点P的直线型隔离带EF,E,F分别在边AB,BC上(隔离带不能穿越湿地,且占地面积忽略不计).设点P到边AD的距离为t(单位:km),△BEF的面积为S(单位:km2).