题目内容
已知椭圆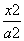 +
+ =1(a>0,b>0)的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
=1(a>0,b>0)的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为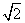 -1.
-1.
(1)求椭圆方程;
(2)已知经过点F的动直线l与椭圆交于不同的两点A,B,点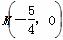 ,证明:
,证明: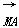 ·
· 为定值.
为定值.
解 (1)化圆的标准方程为(x+1)2+y2=1,
则圆心为(-1,0),半径r=1,所以椭圆的半焦距c=1.
又椭圆上的点到点F的距离最小值为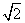 -1,所以a-c=
-1,所以a-c=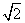 -1,即a=
-1,即a=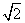 .
.
故所求椭圆的方程为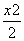 +y2=1.
+y2=1.
(2)①当直线l与x轴垂直时,l的方程为x=-1.
可求得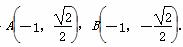
此时,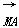 ·
· =
=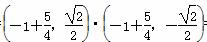 =-
=-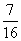 .
.
②当直线l与x轴不垂直时,设直线l的方程为y=k(x+1),
由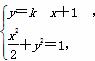 得(1+2k2)x2+4k2x+2k2-2=0,
得(1+2k2)x2+4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),则x1+x2=-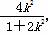 ,x1x2=
,x1x2=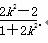 .
.
因为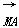 ·
· =
=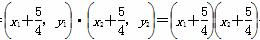 +y1y2
+y1y2
=x1x2+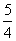 (x1+x2)+
(x1+x2)+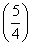 2+k(x1+1)·k(x2+1)
2+k(x1+1)·k(x2+1)
=(1+k2)x1x2+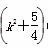 (x1+x2)+k2+
(x1+x2)+k2+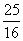
=(1+k2)·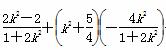 +k2+
+k2+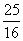
=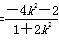 +
+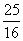 =-2+
=-2+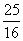 =-
=-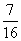 .
.
所以,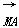 ·
· 为定值,且定值为-
为定值,且定值为-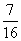 .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
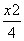 -
-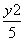 =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=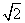 |AF|,则A点的横坐标为( ).
|AF|,则A点的横坐标为( ).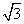 D.4
D.4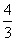 x;④y=2x+1,其中为“R型直线”的是( ).
x;④y=2x+1,其中为“R型直线”的是( ). 第一象限
第一象限  第二象限
第二象限  第三象限
第三象限  第四象限
第四象限 的展开式中的常数项为( )
的展开式中的常数项为( )
