题目内容

4．某校1200名学生中，O型血有450人，A型血有a人，B型血有b人，AB型血有c人，且450，a，b，c成等差数列，为了研究血型与血虚的关系，从中抽取容量为48的样本，按照分层抽样的方法抽取样本，则要抽取的A型血的人数为14．

分析 由题意，利用450，a，b，c成等差数列，求出a，利用分层抽样的定义求出要抽取的A型血的人数．

解答 解：由题意知450，a，b，c成等差数列，设公差为d，
则4×450+$\frac{4×3}{2}$d=1200，∴d=-100，
∴a=350，
从中抽取容量为48的样本，按照分层抽样的方法抽取样本，
则要抽取的A型血的人数为$\frac{350}{1200}×48$=14．
故答案为：14．

点评 本题是等差数列的性质和分层抽样的定义，即样本和总体的结构一致性，求出A型血是关键．

练习册系列答案
相关题目
14．已知函数f（x）=2+$\frac{|x|-x}{3}$（-3＜x≤3）．
（1）用分段函数的形式表示该函数；
（2）画出该函数的图象；
（3）写出该函数的值域．
15．已知函数f（x）=2sin$（ω\;x-\frac{π}{6}$）•cosω$x+\frac{1}{2}$（其中ω＞0）的最小正周期为π．
（Ⅰ） 求ω的值；
（Ⅱ） 将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位，再将所得图象上各点的横坐标伸长为原来的2倍，纵坐标不变，得到函数g（x）的图象．求函数g（x）在[-π，π]上零点．
12．在等比数列{an}中，a1，a4是方程x2-2x-3=0的两根，则a2•a3=（　　）
A．2B．-2C．3D．-3
19．已知f（x）是定义在R上的偶函数，且满足xf′（x）＜0（x≠0），设a=f$（{log_{\frac{1}{4}}}7）$，b=f（log23），c=f（0.2-0.6），则a，b，c的大小关系是（　　）
A．c＜a＜bB．c＜b＜aC．b＜c＜aD．a＜b＜c
9．设f（x）=$\left\{{\begin{array}{l}{-2{e^{x-2}}，x≥2}\\{{{log}_3}（{{x^2}-1}），x＜2}\end{array}}$，则f（f（2））的值为（　　）
A．0B．1C．2D．3
16．在矩形中ABCD中，AB=2AD，在CD上任取一点P，△ABP的最大边是AB的概率是（　　）
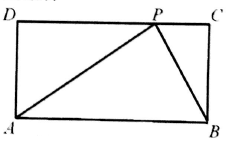
A．$\frac{\sqrt{2}}{2}$B．$\frac{\sqrt{3}}{2}$C．$\sqrt{2}-1$D．$\sqrt{3}-1$
13．已知函数f（x）=ax2+bx-lnx（a，b∈R）．
（1）当a=-1，b=3时，求函数f（x）在[$\frac{1}{2}$，2]上的最大值和最小值；
（2）设a＞0，且对于任意的x＞0，f（x）≥f（1），试比较lna与-2b的大小．
14．已知函数f（x）=x3-3x+5，当x∈[-2，2]时，f（x）＜m恒成立，则实数m的取值范围为m＞7．．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网