题目内容
14.已知函数f(x)=2+$\frac{|x|-x}{3}$(-3<x≤3).(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的值域.
分析 (1)根据题意,由x的范围结合绝对值的意义,当0≤x≤3时,f(x)=2+$\frac{x-x}{3}$=2,当-3<x<0时,f(x)=2+$\frac{-x-x}{3}$=2-$\frac{2}{3}$x,进而综合可得答案;
(2)由(1)的解析式,作出函数的图象即可;
(3)由(2)的图象,分析即可得答案.
解答 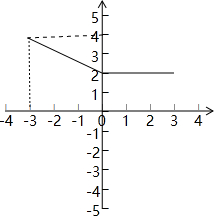 解:(1)当0≤x≤3时,f(x)=2+$\frac{x-x}{3}$=2,
解:(1)当0≤x≤3时,f(x)=2+$\frac{x-x}{3}$=2,
当-3<x<0时,f(x)=2+$\frac{-x-x}{3}$=2-$\frac{2}{3}$x,
∴f(x)=$\left\{{\begin{array}{l}{2,\;\;\;\;\;\;\;\;\;\;0≤x≤3}\\{2-\frac{2}{3}x,-3<x<0}\end{array}}\right.$;
(2)函数f(x)的图象如图所示,
(3)由(2)知,f(x)在(-3,3]上的值域为[2,4).
点评 本题考查分段函数的应用,关键是正确求出该分段函数的解析式,并由此作出函数的图象.

练习册系列答案
相关题目
9.《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(即百分比)为“衰分比”.如:甲、乙、丙、丁分别分得100,60,36,21.6,递减的比例为40%,那么“衰分比”就等于40%,今共有粮a(a>0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丙分得36石,乙、丁所得之和为75石,则“衰分比”与a的值分别是( )
| A. | 75%,$\frac{525}{4}$ | B. | 25%,$\frac{525}{4}$ | C. | 75%,175 | D. | 25%,175 |
6.已知函数y=|x-4|-|x-6|,则当其取最小值时,自变量x的取值范围是( )
| A. | [4,6] | B. | [6,+∞) | C. | (-∞,4] | D. | (4,6) |