题目内容
16.在矩形中ABCD中,AB=2AD,在CD上任取一点P,△ABP的最大边是AB的概率是( )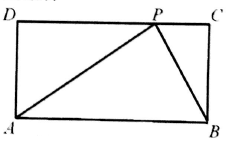
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
分析 分别以A、B为圆心,AB为半径作弧,交C、D于P1,P2,△ABP的最大边是AB的概率p=$\frac{{P}_{1}{P}_{2}}{CD}$,由此利用几何概型能求出结果.
解答 解:分别以A、B为圆心,AB为半径作弧,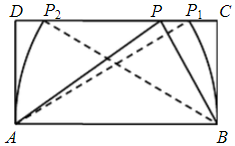
交C、D于P1,P2,
当P在线段P1P2间运动时,能使得△ABP的最大边为AB,
∵在矩形中ABCD中,AB=2AD,设AB=2AD=2,
∴AP1=BP2=2,∴CP1=DP2=2-$\sqrt{4-1}$=2-$\sqrt{3}$,
∴P1P2=2-2(2-$\sqrt{3}$)=2$\sqrt{3}$-2,
∴△ABP的最大边是AB的概率:
p=$\frac{{P}_{1}{P}_{2}}{CD}$=$\sqrt{3}-1$.
故选:D.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意几何概型计算公式的合理运用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
6.已知函数y=|x-4|-|x-6|,则当其取最小值时,自变量x的取值范围是( )
| A. | [4,6] | B. | [6,+∞) | C. | (-∞,4] | D. | (4,6) |
11.已知函数f(x)=$\left\{{\begin{array}{l}{\frac{k}{x},x≥2}\\{{{({x-1})}^2},x<2}\end{array}}$,若方程f(x)=$\frac{1}{2}$有三个不同的实根,则实数k的范围是( )
| A. | (1,2] | B. | [1,+∞) | C. | [1,2) | D. | [1,2] |
8.将函数f(x)=sin(2x+φ)+$\sqrt{3}$cos(2x+φ)(0<φ<π)的图象向左平移$\frac{π}{4}$个单位后,得到的函数的图象关于点$(\frac{π}{2},0)$对称,则函数$g(x)=\frac{1}{2}sin(2x+φ)$在$[-\frac{π}{2},\frac{π}{6}]$上的最小值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |