题目内容
5.在平面直角坐标系xOy中,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左焦点,点P在椭圆上,直线PF与以OF为直径的圆相交于点M(异于点F),若点M为PF的中点,且直线PF的斜率为$\sqrt{3}$,则椭圆的离心率为$\sqrt{3}$-1.分析 由C为OF的中点,则OM为△FOP的中位线,丨OP丨=2丨OM丨=c,∠PFO=60°,△FPO为等边三角形,边长为c,P(-$\frac{1}{2}$c,$\frac{\sqrt{3}}{2}$c),代入椭圆方程:$\frac{{c}^{2}}{4{a}^{2}}$+$\frac{3{c}^{2}}{4{b}^{2}}$=1,由b2=a2-c2,e=$\frac{c}{a}$,0<e<1,即可求得椭圆的离心率.
解答 解:由题意可知:C为OF的中点,则OM为△FOP的中位线,
丨OP丨=2丨OM丨=2丨OC丨=丨OF丨=c,
且直线PF的斜率为$\sqrt{3}$,则∠PFO=60°,
∴△FPO为等边三角形,边长为c,
则P(-$\frac{1}{2}$c,$\frac{\sqrt{3}}{2}$c),代入椭圆方程:$\frac{{c}^{2}}{4{a}^{2}}$+$\frac{3{c}^{2}}{4{b}^{2}}$=1,
由b2=a2-c2,e=$\frac{c}{a}$,
则e4-8e2+4=0,解得:e2=4±2$\sqrt{3}$,
由0<e<1,
解得:e=$\sqrt{3}$-1,
椭圆的离心率$\sqrt{3}$-1,
故答案为:$\sqrt{3}$-1.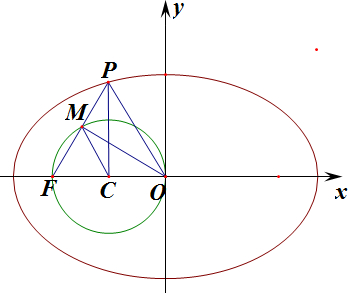
点评 本题考查椭圆的标准方程及简单几何性质,三角形中位线的性质,考查数形结合思想,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
15.已知定义在(0,+∞)的函数f(x),其导函数为f′(x),满足:f(x)>0且$\frac{2x+3}{x}>-\frac{{{f^'}(x)}}{f(x)}$总成立,则下列不等式成立的是( )
| A. | e2e+3f(e)<e2ππ3f(π) | B. | e2e+3f(π)>e2ππ3f(e) | C. | e2e+3f(π)<e2ππ3f(e) | D. | e2e+3f(e)>e2ππ3f(π) |
16.椭圆C的中心在原点,焦点F1,F2在x轴上,椭圆上的点到左焦点F1的距离的最大值为8,过F1的直线交椭圆C于A,B两点,且△ABF2的周长为20,则椭圆C的方程为( )
| A. | $\frac{y^2}{25}+\frac{x^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ |
13.若定义域为R的函数f(x)满足:对任意两个不相等的实数x1,x2,都有$\frac{{{x_2}f({x_1})-{x_1}f({x_2})}}{{{x_1}-{x_2}}}<0$,记:a=4f(0.25),b=0.5f(2),c=0.2f(5),则( )
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | c>b>a |
3.已知函数f(x)=$\left\{\begin{array}{l}{sinx,x≥0}\\{-{x}^{2}-1,x<0}\end{array}\right.$,若f(x)≤kx,则k的范围为( )
| A. | [1,2] | B. | [$\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,1] | D. | (-∞,1) |