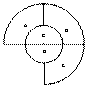
题目内容
如图所示,已知C为圆(x+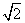 )2+y2=4的圆心,点A(
)2+y2=4的圆心,点A(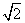 ,0),P是圆上的动点,
,0),P是圆上的动点,
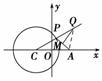 点Q在直线CP上,且
点Q在直线CP上,且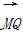 ·
·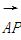 =0,
=0,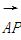 =2
=2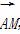 .当点P在圆上运动时,求点Q的轨迹方程.
.当点P在圆上运动时,求点Q的轨迹方程.
解 圆(x+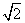 )2+y2=4的圆心为C(-
)2+y2=4的圆心为C(-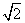 ,0),半径r=2,
,0),半径r=2,
∵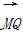 ·
·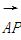 =0,
=0,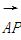 =2
=2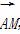 ,
,
∴MQ⊥AP,点M是线段AP的中点,即MQ是AP的中垂线,连接AQ,则|AQ|=|QP|,
∴||QC|-|QA||=||QC|-|QP||=|CP|=r=2,
又|AC|=2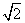 >2,根据双曲线的定义,点Q的轨迹是以C(-
>2,根据双曲线的定义,点Q的轨迹是以C(-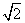 ,0),A(
,0),A(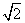 ,0)为焦点,实轴长为2的双曲线,由c=
,0)为焦点,实轴长为2的双曲线,由c=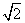 ,a=1,得b2=1,因此点Q的轨迹方程为x2-y2=1.
,a=1,得b2=1,因此点Q的轨迹方程为x2-y2=1.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
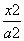 +
+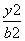 =1(a>b>0)的左、右焦点,过F1倾斜角为45°的直线l与该椭圆相交于P,Q两点,且|PQ|=
=1(a>b>0)的左、右焦点,过F1倾斜角为45°的直线l与该椭圆相交于P,Q两点,且|PQ|=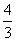 a.
a.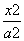 -
-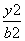 =1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是( ).
=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是( ).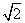 ,2) C.(
,2) C.(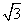 ,2) D.(2,3)
,2) D.(2,3)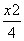 +
+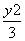 =1的右焦点为F,抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的倾斜角为120°,那么|PF|=________.
=1的右焦点为F,抛物线y2=4x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的倾斜角为120°,那么|PF|=________. 这五个区域内,要求有公共边的两块相邻区域不同的植物,则不同的种法共有( )
这五个区域内,要求有公共边的两块相邻区域不同的植物,则不同的种法共有( )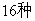 B.
B. 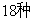 C.
C. 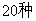 D.
D.