题目内容
4.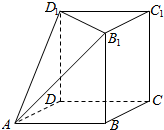 如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.
如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.(1)求异面直线AB1与BC所成角的大小;
(2)求该几何体的体积.
分析 (1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,由此能求出异面直线AB1与BC所成角.
(2)该几何体的体积V=${V}_{A-BD{D}_{1}{B}_{1}}$+${V}_{BDC-{B}_{1}{D}_{1}{C}_{1}}$.
解答 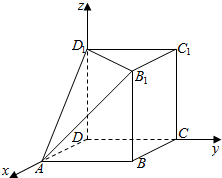 解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A(2,0,0),B1(2,2,2),B(2,2,0),C(0,2,0),
$\overrightarrow{A{B}_{1}}$=(0,2,2),$\overrightarrow{BC}$=(-2,0,0),
设异面直线AB1与BC所成角为θ,
cosθ=$\frac{|\overrightarrow{A{B}_{1}}•\overrightarrow{BC}|}{|\overrightarrow{A{B}_{1}}|•|\overrightarrow{BC}|}$=0,∴θ=90°,
∴异面直线AB1与BC所成角为90°.
(2)该几何体的体积:
V=${V}_{A-BD{D}_{1}{B}_{1}}$+${V}_{BDC-{B}_{1}{D}_{1}{C}_{1}}$
=$\frac{1}{3}×{S}_{四边形BD{D}_{1}{B}_{1}}$×$\frac{AC}{2}$+S△ABC•BB1
=$\frac{1}{3}×2×2\sqrt{2}×\sqrt{2}$+$\frac{1}{2}×2×2×2$
=$\frac{20}{3}$.
点评 本题考查异面直线所成角的大小的求法,考查几何体的体积的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
19.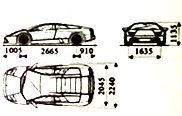 髙先生新购买了辆小汽车,汽车的一些参数如图所示(单位:毫米),他计划把车放在车库地面的中间,四周边缘外前后左右各留半米且上方留空一米,则该车库的体积(保留小数点后两位数字)至少为( )
髙先生新购买了辆小汽车,汽车的一些参数如图所示(单位:毫米),他计划把车放在车库地面的中间,四周边缘外前后左右各留半米且上方留空一米,则该车库的体积(保留小数点后两位数字)至少为( )
 髙先生新购买了辆小汽车,汽车的一些参数如图所示(单位:毫米),他计划把车放在车库地面的中间,四周边缘外前后左右各留半米且上方留空一米,则该车库的体积(保留小数点后两位数字)至少为( )
髙先生新购买了辆小汽车,汽车的一些参数如图所示(单位:毫米),他计划把车放在车库地面的中间,四周边缘外前后左右各留半米且上方留空一米,则该车库的体积(保留小数点后两位数字)至少为( )| A. | 11.64立方米 | B. | 36.28立方米 | C. | 38.60立方米 | D. | 40.70立方米 |
16.已知p是“?x>0,使f(x)=x+$\frac{|a-3|}{x}$的值小于2”的否定.q是“g(x)=ax2-2x在[$\frac{1}{4}$,$\frac{1}{2}$]上单调”,则p是q的( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=-2(用数字作答).
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=-2(用数字作答).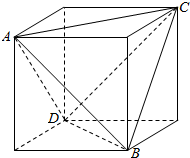 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?
从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?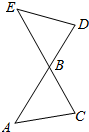 如图所示,某公园计划用鹅卵石铺成两条交叉的“健康石道”(线段AD和CE),并在这两条“健康石道”两端之间建设“花卉长廊”(线段AC和ED),以供市民休闲健身.已铺设好的部分BD=20m,ED=10$\sqrt{6}$m,∠BED=45°(△BDE为锐角三角形).由于设计要求,未铺设好的部分AB和BC的总长只能为40m,则剩余的“花卉长廊”(线段AC)最短可以是20m.
如图所示,某公园计划用鹅卵石铺成两条交叉的“健康石道”(线段AD和CE),并在这两条“健康石道”两端之间建设“花卉长廊”(线段AC和ED),以供市民休闲健身.已铺设好的部分BD=20m,ED=10$\sqrt{6}$m,∠BED=45°(△BDE为锐角三角形).由于设计要求,未铺设好的部分AB和BC的总长只能为40m,则剩余的“花卉长廊”(线段AC)最短可以是20m.