题目内容
设集合A为方程-x2-2x+8=0的解集,集合B为不等式ax-1≤0的解集.
(1)当a=1时,求A∩B;
(2)若A⊆B,求实数a的取值范围.
(1)当a=1时,求A∩B;
(2)若A⊆B,求实数a的取值范围.
考点:集合的包含关系判断及应用,一元二次不等式的解法
专题:集合
分析:(1)通过解方程求出集合A,将a=1代入ax-1≤0,求出集合B,从而求出A∩B;(2)由题意得不等式组,解出即可.
解答:
解:(1)由-x2-2x+8=0,解得A={-4,2},
a=1时,B=(-∞,1],
∴A∩B={-4};
(2)∵A⊆B,
∴
解得:-
≤a≤
.
a=1时,B=(-∞,1],
∴A∩B={-4};
(2)∵A⊆B,
∴
|
解得:-
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查了集合的包含关系,考查了不等式的解法,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系xOy中,如果菱形OABC的边长为2,点B在y轴上,则菱形内(不含边界)的整点(横纵坐标都是整数的点)个数的取值集合是( )
| A、{1,3} |
| B、{0,1,3} |
| C、{0,1,3,4} |
| D、{0,1,2,3,4} |
在平面直角坐标系中,椭圆
+
=1(a>b>0)的焦距为2c(c>0),以O为圆心,a为半径作圆,过点(
,0)作圆的两条切线互相垂直,则离心率e为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )
甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )| A、甲乙同学的平均成绩相同,但是甲同学的成绩比乙稳定 |
| B、甲乙同学的平均成绩相同,但是乙同学的成绩比甲稳定 |
| C、甲同学的平均成绩比乙同学好,但是乙同学的成绩比甲稳定 |
| D、乙同学的平均成绩比甲同学好,但是甲同学的成绩比乙稳定 |
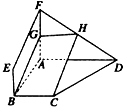 如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BE∥AF,BC∥AD,BC=
如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BE∥AF,BC∥AD,BC=