题目内容
设x,y∈R,a>1,b>1,若ax=by=2.2a+b=8,则
+
的最大值为( )
| 1 |
| x |
| 1 |
| y |
| A、2 | B、3 |
| C、4 | D、log23 |
考点:基本不等式在最值问题中的应用
专题:不等式的解法及应用
分析:由ax=by=2,求出x,y,进而可表示
+
,再利用基本不等式,即可求
+
的最大值.
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
解答:
解:∵ax=by=2,∴x=loga2,y=logb2
∴
=log2a,
=log2b,
∴
+
=log2a+log2b=log2ab,
∵2a+b=8≥2
,
∴ab≤8(当且仅当2a=b时,取等号),
∴
+
≤log28=3,即
+
的最大值为3.
故选B.
∴
| 1 |
| x |
| 1 |
| y |
∴
| 1 |
| x |
| 1 |
| y |
∵2a+b=8≥2
| 2a•b |
∴ab≤8(当且仅当2a=b时,取等号),
∴
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
故选B.
点评:本题考查基本不等式的运用,考查对数运算,考查学生分析转化问题的能力,正确表示
+
是关键.
| 1 |
| x |
| 1 |
| y |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图是一个正三角形场地,如果在每边上放2盆花共需要3盆花;如果在每边上放3盆花共需要6盆花,如果在每边上放n(n>1)盆花,那么共需要花( )盆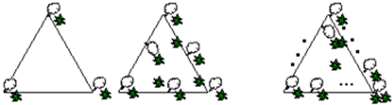

| A、3n | B、3n-1 |
| C、3n-2 | D、3n-3 |
关于x不等式|x-3|+|x+1|≤t2-3t的解集非空,则实数t的取值范围为( )
| A、(-∞,-1]∪[4,+∞) |
| B、(-∞,-2]∪[5,+∞) |
| C、[-1,4] |
| D、(-∞,-1]∪[2,+∞) |
已知△ABC中,内角A,B,C所对边长分别为a,b,c,若A=
,b=2acosB,c=1,则△ABC的面积等于( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知sinα+cosα=
,且0<α<π,则tanα的值为( )
| 1 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|