题目内容
10.已知直线l的参数方程为$\left\{\begin{array}{l}x=\sqrt{3}-\frac{{\sqrt{3}}}{2}t\\ y=1+\frac{1}{2}t\end{array}\right.$(t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为$ρ=4cos(θ-\frac{π}{6})$.(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面$ρ≤4cos(θ-\frac{π}{6})$的公共点,求$μ=\sqrt{3}x+y$的取值范围.
分析 (Ⅰ)圆C的极坐标方程转化为${ρ^2}=4ρ(\frac{{\sqrt{3}}}{2}cosθ+\frac{1}{2}sinθ)$,由此能求出圆C的直角坐标方程.
(Ⅱ)由圆C的方程转化为${(x-\sqrt{3})^2}+{(y-1)^2}=4$,得到圆C的圆心是$(\sqrt{3},1)$,半径是2,将$\left\{{\begin{array}{l}{x=\sqrt{3}-\frac{{\sqrt{3}}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}}\right.$,代入$u=\sqrt{3}x+y$,得u=4-t,由此能求出$u=\sqrt{3}x+y$的取值范围.
解答 解:(Ⅰ)因为圆C的极坐标方程为$ρ=4cos(θ-\frac{π}{6})$,
所以${ρ^2}=4ρ(\frac{{\sqrt{3}}}{2}cosθ+\frac{1}{2}sinθ)$
所以圆C的直角坐标方程${x^2}+{y^2}-2\sqrt{3}x-2y=0$.
(Ⅱ)由圆C的方程${x^2}+{y^2}-2\sqrt{3}x-2y=0$,可得${(x-\sqrt{3})^2}+{(y-1)^2}=4$,
所以圆C的圆心是$(\sqrt{3},1)$,半径是2,
将$\left\{{\begin{array}{l}{x=\sqrt{3}-\frac{{\sqrt{3}}}{2}t}\\{y=1+\frac{1}{2}t}\end{array}}\right.$,代入$u=\sqrt{3}x+y$,得u=4-t,
又直线l过$C(\sqrt{3},1)$,圆C的半径是2,所以-2≤t≤2,
即$u=\sqrt{3}x+y$的取值范围是[2,6].
点评 本题考查圆的直角坐标的求法,考查代数式的取值范围的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | $6\sqrt{3}$ | B. | $4\sqrt{7}$ | C. | $8\sqrt{7}$ | D. | 12 |

| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{5}$,PB=$\sqrt{7}$
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{5}$,PB=$\sqrt{7}$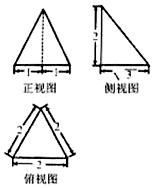 某几何体的三视图如图所示,则该几何体最长的一条棱的长度=2$\sqrt{2}$,体积为$\frac{2\sqrt{3}}{3}$.
某几何体的三视图如图所示,则该几何体最长的一条棱的长度=2$\sqrt{2}$,体积为$\frac{2\sqrt{3}}{3}$.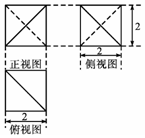 如图是某多面体的三视图,则该几何体的外接球体积为4$\sqrt{3}$π.
如图是某多面体的三视图,则该几何体的外接球体积为4$\sqrt{3}$π.