题目内容
1.在△ABC中,AB=2,AC=3,∠BAC=90°,点D在AB上,点E在CD上,且∠ACB=∠DBE=∠DEB,则DC=$\frac{13}{4}$.分析 如图所示,过点E,做EF⊥AB,垂足为F,设BD=x,∠ACB=∠DBE=∠DEB=θ,先求出tanθ=$\frac{2}{3}$,再求出tan2θ,根据两直线平行可得$\frac{xcos2θ}{2-x}$=$\frac{xsin2θ}{3}$,求出x的在值,再根据勾股定理求出答案.
解答  解:如图所示,过点E,做EF⊥AB,垂足为F,
解:如图所示,过点E,做EF⊥AB,垂足为F,
设BD=x,∠ACB=∠DBE=∠DEB=θ,
∵AB=2,AC=3,∠BAC=90°,
∴tanθ=$\frac{2}{3}$,
∵∠DBE=∠DEB=θ
∴∠EDF=∠DBE+∠DEB=2θ,
∴tan2θ=$\frac{2tanθ}{1-ta{n}^{2}θ}$=$\frac{2×\frac{2}{3}}{1-\frac{4}{9}}$=$\frac{12}{5}$,
在Rt△EFD中,EF=xsin2θ,DF=xcos2θ
∵EF∥AC,
∴$\frac{DF}{AD}$=$\frac{EF}{AC}$,
∴$\frac{xcos2θ}{2-x}$=$\frac{xsin2θ}{3}$,
解得x=$\frac{3}{4}$,
∴AD=2-x=$\frac{5}{4}$,
∴CD=$\sqrt{A{C}^{2}+A{D}^{2}}$=$\sqrt{9+\frac{25}{16}}$=$\frac{13}{4}$,
故答案为:$\frac{13}{4}$.
点评 本题考查了解三角形的有关知识和两角和的正切公式以及相似的问题,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
12.把-1485°化为α+2kπ(k∈Z,0≤α≤2π)的形式是( )
| A. | $\frac{π}{4}$-8π | B. | -$\frac{7}{4}$π-8π | C. | -$\frac{π}{4}$-10π | D. | -10π+$\frac{7π}{4}$ |
6.在区间[1,5]和[2,4]上分别各取一个数,记为m和n,则方程$\frac{x^2}{m^2}+\frac{y^2}{n^2}=1$表示焦点在x轴上的椭圆的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
13.若直线x-y-2=0被圆(x-a)2+y2=4所截得的弦长为$2\sqrt{2}$,则实数a为( )
| A. | -1或$\sqrt{3}$ | B. | 1或3 | C. | -2或6 | D. | 0或4 |
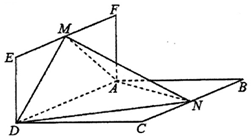 如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M,N分别是EF,BC的中点,AB=2AF,∠CBA=
如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M,N分别是EF,BC的中点,AB=2AF,∠CBA=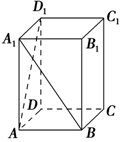 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2AB=2BC,求异面直线A1B与AD1所成角的余弦值.