题目内容
圆心在直线l：x-y+1=0上，且过A（1，1），B（2，-2）两点的圆的方程为（ ）
| A、（x-3）2+（y-2）2=25 |
| B、（x+3）2+（y-2）2=25 |
| C、（x-3）2+（y+2）2=25 |
| D、（x+3）2+（y+2）2=25 |
考点：圆的标准方程
专题：直线与圆
分析：设圆心为C（m，m+1），再根据CA2=CB2 求得m的值，可得圆心坐标以及半径的平方CA2 的值，从而求得圆的标准方程．
解答：
解：由于圆心在直线l：x-y+1=0上，可设圆心为C（m，m+1），
再根据圆过A（1，1），B（2，-2）两点，可得CA2=（m-1）2+（m+1-1）2=CB2=（m-2）2+（m+1+2）2，
求得 m=-3，故圆心为（-3，-2），半径的平方CA2=25，
故圆的方程为 （x+3）2+（y+2）2=25，
故选：D．
再根据圆过A（1，1），B（2，-2）两点，可得CA2=（m-1）2+（m+1-1）2=CB2=（m-2）2+（m+1+2）2，
求得 m=-3，故圆心为（-3，-2），半径的平方CA2=25，
故圆的方程为 （x+3）2+（y+2）2=25，
故选：D．
点评：本题主要考查求圆的标准方程的方法，求出圆心坐标和半径的值，是解题的关键，属于基础题．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
集合A={x|2x-3≤0}，B={x|-1≤x＜2}，则A∪B=（ ）
A、{x|-
| ||
| B、{x|x＜2} | ||
C、{x|-1≤x＜
| ||
D、{x|x≤
|
李明所在的高二（16）班有58名学生，学校要从该班抽出5人开座谈会，若采用系统抽样法，需先剔除3人，再将留下的55人平均分成5个组，每组各抽一人，则李明参加座谈会的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
“a＞b”是“ac2＞bc2”的（ ）
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
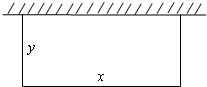一段长为20米的篱笆围成一个一边靠墙的矩形菜园，墙长18米．如图，设菜园与墙平行的边长为x米，另一边长为y米．