题目内容
已知直线l:x-y+1=0和点A(1,0)
(Ⅰ)过点A作直线l的垂线,垂足为B,求点B的坐标;
(Ⅱ)若直线l与x轴的交点为C,将△ABC绕直线l旋转一周,求所得几何体的表面积.
(Ⅰ)过点A作直线l的垂线,垂足为B,求点B的坐标;
(Ⅱ)若直线l与x轴的交点为C,将△ABC绕直线l旋转一周,求所得几何体的表面积.
考点:扇形面积公式,弧度制的应用
专题:综合题,直线与圆
分析:(Ⅰ)根据直线垂直的条件求出直线AB的斜率,再代入点斜式方程进行化简,再联立两个直线方程求出点B的坐标;
(Ⅱ)求出点C的坐标并画出图象,再判断出旋转后所得的几何体是圆锥,由图求出底面的半径和母线长,代入表面积公式求解.
(Ⅱ)求出点C的坐标并画出图象,再判断出旋转后所得的几何体是圆锥,由图求出底面的半径和母线长,代入表面积公式求解.
解答:
 解:(Ⅰ)由题意得,直线AB的斜率为-1,且过A(1,0),
解:(Ⅰ)由题意得,直线AB的斜率为-1,且过A(1,0),
∴直线AB的方程为:y=-(x-1),即x+y-1=0,
由
得,x=0、y=1,故B(0,1),
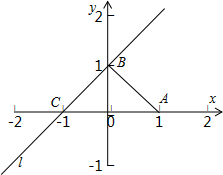
(Ⅱ)根据题意画出图象如右图:
令y=0代入x-y+1=0得,x=-1,则C(-1,0),
将△ABC绕直线l旋转一周得圆锥,
其底面的半径r=|AB|=
,
母线为l=|AC|=2,
∴几何体的表面积S=πrl+πr2
=(2
+2)π.
 解:(Ⅰ)由题意得,直线AB的斜率为-1,且过A(1,0),
解:(Ⅰ)由题意得,直线AB的斜率为-1,且过A(1,0),∴直线AB的方程为:y=-(x-1),即x+y-1=0,
由
|
(Ⅱ)根据题意画出图象如右图:
令y=0代入x-y+1=0得,x=-1,则C(-1,0),
将△ABC绕直线l旋转一周得圆锥,
其底面的半径r=|AB|=
| 2 |
母线为l=|AC|=2,
∴几何体的表面积S=πrl+πr2
=(2
| 2 |
点评:本题考查了直线垂直的条件、点斜式方程,以及旋转体-圆锥的表面积公式的应用.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
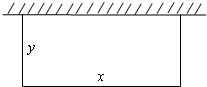 一段长为20米的篱笆围成一个一边靠墙的矩形菜园,墙长18米.如图,设菜园与墙平行的边长为x米,另一边长为y米.
一段长为20米的篱笆围成一个一边靠墙的矩形菜园,墙长18米.如图,设菜园与墙平行的边长为x米,另一边长为y米.