题目内容
18．命题“?x0∈（1，+∞），x02+2x0+2≤0”的否定形式是（ ）| A． | $?x∈（1，+∞），x_0^2+2{x_0}+2＞0$ | B． | $?x∈（{-∞，1}]，x_0^2+2{x_0}+2＞0$ | ||
| C． | $?{x_0}∈（1，+∞），x_0^2+2{x_0}+2＞0$ | D． | $?{x_0}∈（{-∞，1}]，x_0^2+2{x_0}+2＞0$ |
分析 根据特称命题的否定是全称命题，写出它的否定命题即可．
解答 解：命题“?x0∈（1，+∞），x02+2x0+2≤0”的否定形式是：
“?x∈（1，+∞），x2+2x+2＞0”．
故选：A．
点评 本题考查了特称命题的否定是全称命题的应用问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
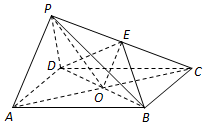如图，在四棱锥P-ABCD中，四边形ABCD为平行四边形，AC，BD相交于点O，点E为PC的中点，OP=OC，PA⊥PD．求证：
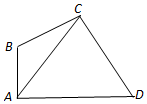如图，在平面四边形ABCD中，AB⊥AD，AB=1，AC=$\sqrt{7}$，△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$，DC=$\frac{{4\sqrt{7}}}{5}$
3．已知$f（x）=\frac{lnx}{x}$，则（ ）
| A． | f（2）＞f（e）＞f（3） | B． | f（3）＞f（e）＞f（2） | C． | f（3）＞f（2）＞f（e） | D． | f（e）＞f（3）＞f（2） |