题目内容
已知关于x的一元二次方程x2-2x+b-a+3=0,其中a、b为常数,点(a,b)是区域Ω:
内的随机点.
(1)当方程无实根且a、b∈N 时,试列举出所有的点(a,b),并求此时概率P1;
(2)设该方程的两个实根分别为x1、x2,试求x1、x2满足 0≤x1≤1≤x2 时的概率P2.
|
(1)当方程无实根且a、b∈N 时,试列举出所有的点(a,b),并求此时概率P1;
(2)设该方程的两个实根分别为x1、x2,试求x1、x2满足 0≤x1≤1≤x2 时的概率P2.
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(1)当方程无实根且a、b∈N 时,利用列举法,即可求出所有的点(a,b),并根据古典概率的概率公式即可求此时概率P1;
(2)把f(x)=0的两个根满足的条件转化为函数f(x)的两个零点满足的条件,分别画出点(a,b)满足的区域Ω及在区域Ω内满足条件0≤x1≤1≤x2的点(a,b)的区域,再利用几何概型的概率计算公式即可得出概率P2.
(2)把f(x)=0的两个根满足的条件转化为函数f(x)的两个零点满足的条件,分别画出点(a,b)满足的区域Ω及在区域Ω内满足条件0≤x1≤1≤x2的点(a,b)的区域,再利用几何概型的概率计算公式即可得出概率P2.
解答:
解:(1)若a,b∈N,则满
的点共有5×5=25个结果,
若方程无实根,则△=4-4(b-a+3)<0,
即a-b<2,∴b>a-2,
则当a=0时,b>-2,此时b=0,1,2,3,4,
当a=1时,b>-1,此时b=0,1,2,3,4,
当a=2时,b>0,此时b=1,2,3,4,
当a=3时,b>1,此时b=2,3,4,
当a=4时,b>2,此时b=3,4,
则满足条件的点共有(0,1),(0,2),(0,3),(0,4),(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,2),(3,3),(3,4),(4,3),(4,4),共有19个结果,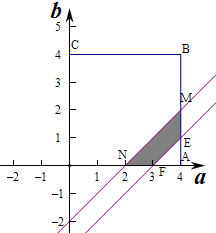
则根据古典概率的公式可知此时概率P1=
.
(2)令f(x)=x2-2x+b-a+3,由方程f(x)=0的两个实数根分别为x1、x2且x1、x2满足0≤x1≤1≤x2,
则根据二次函数根的分布可知,函数f(x)分别在区间(0,1]、[1,+∞)各有一个零点.
即
,即
.
分别画出点(a,b)满足的区域Ω:
,
在区域Ω内满足条件0≤x1≤1≤x2的点(a,b)的区域如图.
区域Ω的面积=4×4=16,梯形EFMN的面积=S△AMN-S△AEF=
×2×2-
×1×1=
∴方程f(x)=0的两个实数根分别为x1、x2且x1、x2满足0≤x1≤1≤x2的事件的概率P2=
=
.
|
若方程无实根,则△=4-4(b-a+3)<0,
即a-b<2,∴b>a-2,
则当a=0时,b>-2,此时b=0,1,2,3,4,
当a=1时,b>-1,此时b=0,1,2,3,4,
当a=2时,b>0,此时b=1,2,3,4,
当a=3时,b>1,此时b=2,3,4,
当a=4时,b>2,此时b=3,4,
则满足条件的点共有(0,1),(0,2),(0,3),(0,4),(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,2),(3,3),(3,4),(4,3),(4,4),共有19个结果,

则根据古典概率的公式可知此时概率P1=
| 19 |
| 25 |
(2)令f(x)=x2-2x+b-a+3,由方程f(x)=0的两个实数根分别为x1、x2且x1、x2满足0≤x1≤1≤x2,
则根据二次函数根的分布可知,函数f(x)分别在区间(0,1]、[1,+∞)各有一个零点.
即
|
|
分别画出点(a,b)满足的区域Ω:
|
在区域Ω内满足条件0≤x1≤1≤x2的点(a,b)的区域如图.
区域Ω的面积=4×4=16,梯形EFMN的面积=S△AMN-S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴方程f(x)=0的两个实数根分别为x1、x2且x1、x2满足0≤x1≤1≤x2的事件的概率P2=
| ||
| 16 |
| 3 |
| 32 |
点评:本题主要考查古典概率和几何概型的概率的计算,考查学生的计算能力,综合性较强.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
等差数列{an}中,a4+a8=10,a10=6,则a18等于( )
| A、7 | B、7.5 | C、8 | D、8.5 |
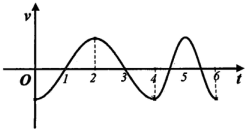
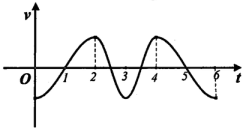
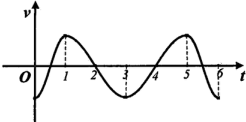
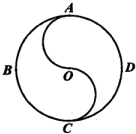 如图,半径为2的圆内有两条半圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度v=v(t)的图象大致为( )
如图,半径为2的圆内有两条半圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度v=v(t)的图象大致为( )