题目内容
已知抛物线C1:y=
x2(p>0)的焦点与双曲线C2:
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
| 1 |
| 2p |
| x2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:由曲线方程求出抛物线与双曲线的焦点坐标,由两点式写出过两个焦点的直线方程,求出函数y=
x2(p>0)在x取直线与抛物线交点M的横坐标时的导数值,由其等于双曲线渐近线的斜率得到交点横坐标与p的关系,把M点的坐标代入直线方程即可求得p的值.
| 1 |
| 2p |
解答:
解:由抛物线C1:y=
x2(p>0)得x2=2py(p>0),
所以抛物线的焦点坐标为F(0,
).
由
-y2=1得a=
,b=1,c=2.
所以双曲线的右焦点为(2,0).
则抛物线的焦点与双曲线的右焦点的连线所在直线方程为
=
,
即
x+2y-p=0①.
设该直线交抛物线于M(x0,
),则C1在点M处的切线的斜率为
.
由题意可知
=
,得x0=
p,代入M点得M(
p,
)
把M点代入①得:
+
p-2p=0.
解得p=
.
故选:D.
| 1 |
| 2p |
所以抛物线的焦点坐标为F(0,
| p |
| 2 |
由
| x2 |
| 3 |
| 3 |
所以双曲线的右焦点为(2,0).
则抛物线的焦点与双曲线的右焦点的连线所在直线方程为
| y-0 | ||
|
| x-2 |
| 0-2 |
即
| p |
| 2 |
设该直线交抛物线于M(x0,
| x02 |
| 2p |
| x0 |
| p |
由题意可知
| x0 |
| p |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| p |
| 6 |
把M点代入①得:
| ||
| 3 |
| 2 |
| 3 |
解得p=
4
| ||
| 3 |
故选:D.
点评:本题考查了双曲线的简单几何性质,考查了利用导数研究曲线上某点的切线方程,函数在曲线上某点处的切线的斜率等于函数在该点处的导数,是中档题.

练习册系列答案
相关题目
已知O为△ABC的外心,|
|=16,|
|=10
,若
=x
+y
,且32x+25y=25,则|
|=( )
| AB |
| AC |
| 2 |
| AO |
| AB |
| AC |
| OA |
| A、8 | B、10 | C、12 | D、14 |
若一个三棱锥有三个面两两垂直,则称此三棱锥为直角三棱锥,在长方体的8个顶点中任取4个点构成的三棱锥中是直角三棱锥的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
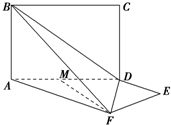 如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为线段AD的中点.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为线段AD的中点.