题目内容
设a=50.8,b=0.67,c=log0.74,则a,b,c的大小关系是( )
| A、a<c<b |
| B、c<a<b |
| C、b<a<c |
| D、c<b<a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:对于a和b,运用指数函数的性质与0,1比较,可知a>1,0<b<1,利用对数函数的单调性得到c<0,从而得到a,b,c的大小.
解答:
解:a=50.8>50=1,0<b=0.67<0.60=1
c=log0.74<log0.71=0,
所以,c<b<a.
故选D.
c=log0.74<log0.71=0,
所以,c<b<a.
故选D.
点评:本题考查了有理指数幂的化简求值和对数值的大小比较,考查了指数函数和对数函数的单调性,该类大小比较问题,有时利用0和1当媒介,往往能起到事半功倍的效果,此题是基础题

练习册系列答案
相关题目
三个数a=(
) -
,b=(
) -
,c=(
) -
的大小顺序是( )
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| A、c<a<b |
| B、c<b<a |
| C、a<b<c |
| D、b<a<c |
已知集合A={x∈Z||x-1|≤1},B={y∈N|y=
,x∈[1,4]},则可建立从集合A到集合B的映射个数为( )
| 2x-2 |
| A、16 | B、27 | C、64 | D、81 |
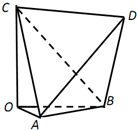 如图,多面体OABCD,AB=CD=2,AD=BC=2
如图,多面体OABCD,AB=CD=2,AD=BC=2