题目内容
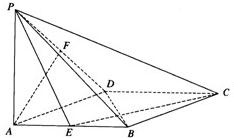 如图,在正方形ABCD中,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.
如图,在正方形ABCD中,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.(1)求证:PC⊥AF;
(2)求证:AF∥平面PEC;
(3)求证:PD⊥平面AFE.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由于AC是斜线PC在平面ABCD上的射影,故可利用三垂线定理,转化为证明:AC⊥BD
(2)要证明AF∥平面PEC,关键是要找到平面PEC中与AF平行的直线
(3)连接FE,因为ABCD是正方形,且PA=AB=2,E、F分别是AB与PD的中点,得到EF⊥PD,AF∩PD,由线面垂直的判定定理判断.
(2)要证明AF∥平面PEC,关键是要找到平面PEC中与AF平行的直线
(3)连接FE,因为ABCD是正方形,且PA=AB=2,E、F分别是AB与PD的中点,得到EF⊥PD,AF∩PD,由线面垂直的判定定理判断.
解答:
解:(1)连接AC,则AC⊥BD.
∵PA⊥平面ABCD,AC是斜线,
PC在平面ABCD上的射影,
∴由三垂线定理得PC⊥BD.
(2)取PC的中点K,连接FK、EK,
则四边形AEKF是平行四边形,
∴AF∥EK,又EK?平面PEC,
AF?平面PEC,
∴AF∥平面PEC.
(3)连接EF,因为ABCD是正方形,且PA=AB=2,E、F分别是AB与PD的中点.
所以PE=DE=
,
所以EF⊥PD,AF∩PD,
所以PD⊥平面AEF.

∵PA⊥平面ABCD,AC是斜线,
PC在平面ABCD上的射影,
∴由三垂线定理得PC⊥BD.
(2)取PC的中点K,连接FK、EK,
则四边形AEKF是平行四边形,
∴AF∥EK,又EK?平面PEC,
AF?平面PEC,
∴AF∥平面PEC.
(3)连接EF,因为ABCD是正方形,且PA=AB=2,E、F分别是AB与PD的中点.
所以PE=DE=
| 5 |
所以EF⊥PD,AF∩PD,
所以PD⊥平面AEF.

点评:本题考查了线面平行、垂直的判定定理和性质定理;
判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a∥α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?β,a∥α⇒a∥β).
判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a∥α,b?α,a∥b⇒a∥α);③利用面面平行的性质定理(α∥β,a?α⇒a∥β);④利用面面平行的性质(α∥β,a?β,a∥α⇒a∥β).

练习册系列答案
相关题目
若椭圆的中心在原点,一个焦点为(0,2),直线y=3x+7与椭圆相交所得弦的中点的纵坐标为1,则这个椭圆的方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从装有2个黄球和2个蓝球的口袋内任取2个球,则恰有一个黄球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分别以直角三角形的斜边和两直角边所在直线为轴,将三角形旋转一周所得旋转体的体积依次为V1、V2、V3,则( )
| A、V1=V2+V3 | ||||||
| B、V12=V22+V32 | ||||||
C、
| ||||||
D、
|
函数y=sin2x的图象向左平移
个单位,得到函数y=f(x)的图象,则下列说法正确的是( )
| π |
| 4 |
| A、y=f(x)是奇函数 | ||
| B、y=f(x)的周期为2π | ||
C、y=f(x)的图象关于x=
| ||
D、y=f(x)的图象关于点(
|

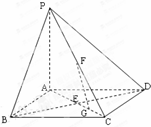 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,BD交AC于点E,F是线段PC中点,G为线段EC中点.