题目内容
公共汽车在8：00到8：20内随机地到达某站，某人8：15到达该站，则他能等到公共汽车的概率为 ．
考点：几何概型
专题：概率与统计
分析：由已知中公共汽车在8：00到8：20内随机地到达某站，某人8：15到达该站，我们可以分别求出所有基本事件对应的时间总长度和事件“他能等到公共汽车”对应的时间总长度，代入几何概型公式可得答案．
解答：
解：∵公共汽车在8：00到8：20内随机地到达某站，
故所有基本事件对应的时间总长度LΩ=20
某人8：15到达该站，
记“他能等到公共汽车”为事件A
则LA=5
故P（A）=
=
；
故答案为
．
故所有基本事件对应的时间总长度LΩ=20
某人8：15到达该站，
记“他能等到公共汽车”为事件A
则LA=5
故P（A）=
| 5 |
| 20 |
| 1 |
| 4 |
故答案为
| 1 |
| 4 |
点评：本题考查的知识点是几何概型，几何概型分长度类，面积类，角度类，体积类，解答的关键是根据已知计算出所有基本事件对应的几何量和满足条件的基本事件对应的几何量
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图为函数f（x）=若a，b∈{-1，0，1，2}，则函数f（x）=ax2+2x+b有零点的概率为 A（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
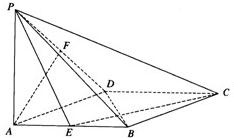如图，在正方形ABCD中，PA⊥底面ABCD，且PA=AB=2，E、F分别是AB与PD的中点．