题目内容
分别以直角三角形的斜边和两直角边所在直线为轴,将三角形旋转一周所得旋转体的体积依次为V1、V2、V3,则( )
| A、V1=V2+V3 | ||||||
| B、V12=V22+V32 | ||||||
C、
| ||||||
D、
|
考点:旋转体(圆柱、圆锥、圆台)
专题:
分析:设直角三角形的三边分别为a、b、c,a2+b2=c2,即c为斜边,分别求得V1、V2、V3的值,可得结论.
解答:
解:设直角三角形的三边分别为a、b、c,a2+b2=c2,即c为斜边,
则以边c所在直线为轴,将三角形旋转一周所得旋转体的体积为V1,则V1 =
π(
)2•c=
πa2•b2•
,
以边a所在直线为轴,将三角形旋转一周所得旋转体的体积为V2,则V2 =
πb2•a,
以边b所在直线为轴,将三角形旋转一周所得旋转体的体积为V3,则V3 =πa2•b,
∴
=
+
,
故选:C.
则以边c所在直线为轴,将三角形旋转一周所得旋转体的体积为V1,则V1 =
| 1 |
| 3 |
| ab |
| c |
| 1 |
| 3 |
| 1 |
| c |
以边a所在直线为轴,将三角形旋转一周所得旋转体的体积为V2,则V2 =
| 1 |
| 3 |
以边b所在直线为轴,将三角形旋转一周所得旋转体的体积为V3,则V3 =πa2•b,
∴
| 1 |
| V12 |
| 1 |
| V22 |
| 1 |
| V22 |
故选:C.
点评:本题考查几何体的体积的求法与大小比较,考查计算能力,属于基础题.

练习册系列答案
相关题目
“x-1≠0”是“(x-1)(x-2)≠0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既不充分也非必要条件 |
已知函数f(x)=sinωx+cosωx,如果存在实数x1,使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2010)成立,则ω的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
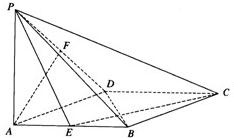 如图,在正方形ABCD中,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.
如图,在正方形ABCD中,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.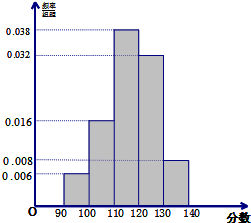 某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组[90,100),第二组[100,110),第五组[130,140].按上述分组方法得到的频率分布直方图如图所示.
某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组[90,100),第二组[100,110),第五组[130,140].按上述分组方法得到的频率分布直方图如图所示.