题目内容
20.已知$\overrightarrow{a}$=($\sqrt{3}$sinωx,cosωx),$\overrightarrow{b}$=(cosωx,cosωx)(ω>0),记函数f(x)=$\vec a$•$\vec b$,且f(x)的最小正周期是π,则ω=( )| A. | ω=1 | B. | ω=2 | C. | ω=$\frac{1}{2}$ | D. | ω=$\frac{2}{3}$ |
分析 根据向量的基本运算把两向量的坐标代入,利用二倍角公式和两角和公式化简整理,
再利用正弦函数的性质求得ω的值.
解答 解:$\overrightarrow{a}$=($\sqrt{3}$sinωx,cosωx),$\overrightarrow{b}$=(cosωx,cosωx)(ω>0),
∴函数f(x)=$\vec a$•$\vec b$=$\sqrt{3}$sinωxcosωx+cos2ωx
=$\frac{\sqrt{3}}{2}$sin2ωx+$\frac{1}{2}$cos2ωx+$\frac{1}{2}$
=sin(2ωx+$\frac{π}{6}$)+$\frac{1}{2}$
依题意可知T=$\frac{2π}{2ω}$=π,求得ω=1.
故选:A.
点评 本题主要考查了三角函数的周期性及其求法,向量的基本运算以及二倍角公式和两角和公式的应用问题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
15.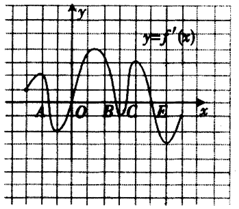 函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )
函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )
 函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )
函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.已知直线l:x+ay-1=0(a∈R)是圆C:x2+y2-4x-2y+1=0的对称轴,过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )
| A. | 2 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{10}$ | D. | 6 |
9.已知f(cosx)=sin3x,则f(sin20°)的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
10.甲、乙、丙、丁四位同学在建立变量x,y的回归模型时,分别选择了4种不同模型,计算可得它们的相关指数R2分别如表:
建立的回归模型拟合效果最差的同学是( )
| 甲 | 乙 | 丙 | 丁 | |
| R2 | 0.98 | 0.78 | 0.50 | 0.85 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |